assignment problem javatpoint

DAA Tutorial
DAA Algorithm
Need of Algorithm
Complexity of Algorithm
Algorithm Design Techniques
Asymptotic Analysis
Analyzing Algorithm Control Structure
Recurrence Relation
Recursion Tree Method
Master Method

Analysis of Sorting

Bubble Sort
Selection Sort
Insertion Sort

Divide and Conquer

Introduction
Max-Min Problem
Binary Search
Tower of Hanoi
Binary Heap
Stable Sorting
Lower bound Theory

Sorting in Linear Time

Linear Time
Counting Sort
Bucket Sort
Hash Tables
Hashing Method
Open Addressing Techniques
Hash Function

Binary Search Trees

Red Black Tree
Dynamic Programming
Divide & Conquer Method vs Dynamic Programming
Fibonacci sequence
Matrix Chain Multiplication
Matrix Chain Multiplication Example
Matrix Chain Multiplication Algorithm
Longest Common Sequence
Longest Common Sequence Algorithm
0/1 Knapsack Problem
DUTCH NATIONAL FLAG
Longest Palindrome Subsequence
Longest Increasing Subsequence
Longest Common Subsequence
Tabulation vs Memoization
How to solve a dynamic programming problem
Optimal Substructure Property
Overlapping sub-problems
Dynamic programming vs Greedy approach
Regular Expression Matching
Branch and bound vs backtracking
Branch and bound
Longest Repeated Subsequence
Longest Common Substring
Shortest Common Supersequence
Dynamic Programming vs Divide and Conquer
Maximum Sum Increasing Subsequence
Wildcard Pattern Matching
Largest Sum Contiguous Subarray
Shortest Sum Contiguous Subarray
Dynamic programming vs Backtracking
Brute force approach
Fractional vs 0/1 knapsack problem
Traveling Salesperson problem using branch and bound
Integer Partition Problem
Kruskal Algorithm

Greedy Algorithm

Greedy Algorithms
Activity Selection Problem
Fractional Knapsack problem
Huffman Codes
Algorithm of Huffman Code
Activity or Task Scheduling Problem
Travelling Sales Person Problem
Dynamic Programming vs Greedy Method

Backtracking

Backtracking Introduction
Recursive Maze Algorithm
Hamiltonian Circuit Problems
Subset Sum Problems
N Queens Problems
MST Introduction
MST Applications
Kruskal's Algorithm
Prim's Algorithm

Shortest Path

Negative Weight Edges
Representing Shortest Path
Dijkstra's Algorithm
Bellman-Ford Algorithm
Single Source Shortest Path in a directed Acyclic Graphs

All-Pairs Shortest Paths

Floyd-Warshall Algorithm
Johnson's Algorithm

Maximum Flow

Flow networks and Flows
Network Flow Problems
Ford Fulkerson Algorithm
Maximum bipartite matching

Sorting Networks

Comparison Network
Bitonic Sorting Network
Merging Network

Complexity Theory

Complexity Classes
Polynomial Time Verification
NP-Completeness
Circuit Satisfiability
3-CNF Satisfiability
Clique Problem
Vertex Cover Problem
Subset-Sum Problem

Approximation Algo

Vertex Cover
Travelling Salesman Problem

String Matching

Naive String Matching Algorithm
Rabin-Karp-Algorithm
String Matching with Finite Automata
Knuth-Morris-Pratt Algorithm
Boyer-Moore Algorithm
Kosaraju Algorithm
Hashing algorithm
Huffman Coding Algorithm
Kadane's Algorithm
Dijkstra Algorithm Example
Euclidean algorithm
Floyd's Algorithm
Properties of Algorithm
Time Complexity of Kruskals Algorithm
Kosaraju's Algorithm
Characteristics of an Algorithm
Algorithm Examples
Searching Algorithms
Algorithm for Binary Search
Sorting Algorithms: Slowest to Fastest
Extended Euclidian Algorithm
How to Write an Algorithm
Recursive Algorithm
Sliding Window Algorithm
Difference Between Algorithms and Flowcharts
PageRank Algorithm
Greedy Algorithm Example
Best Books for Data Structures and Algorithms
Difference between 4 queen and 8 queen problem
Halting Problem in Theory of Computation
Maximum Subarray Sum of Alternate Parity

Interview Questions

DAA Interview Questions

Latest Courses

We provides tutorials and interview questions of all technology like java tutorial, android, java frameworks

Contact info

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

[email protected] .

Online Compiler

Branch and Bound Tutorial
Backtracking Vs Branch-N-Bound
0/1 Knapsack
8 Puzzle Problem
Job Assignment Problem
N-Queen Problem
Travelling Salesman Problem

Job Assignment Problem using Branch And Bound

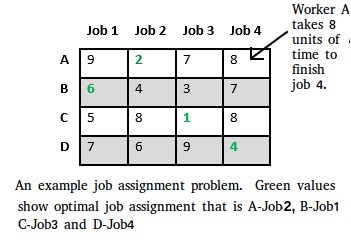
Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

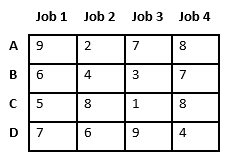
Let us explore all approaches for this problem.

Solution 1: Brute Force

We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm

The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree

A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound

The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:

For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

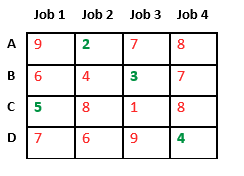
Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A.

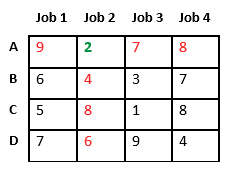
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red).

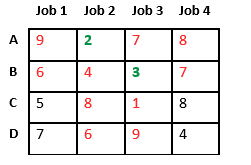
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable.

Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14.

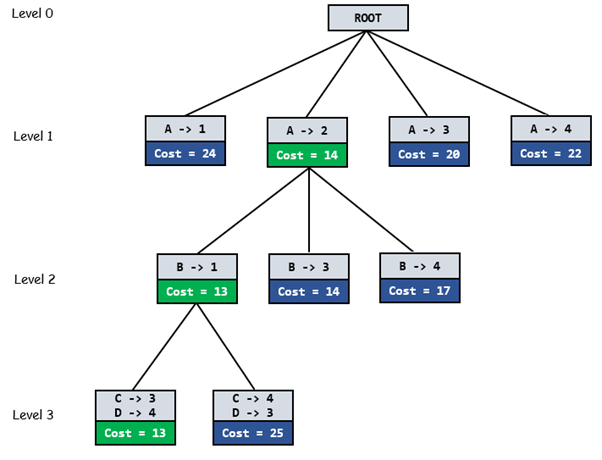
Below diagram shows complete search space diagram showing optimal solution path in green.

Complete Algorithm:

Below is the implementation of the above approach:

Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix. Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.