meaning of assignment model

MBA Knowledge Base

Business • Management • Technology

Home » Management Science » Transportation and Assignment Models in Operations Research

Transportation and Assignment Models in Operations Research

Transportation and assignment models are special purpose algorithms of the linear programming. The simplex method of Linear Programming Problems(LPP) proves to be inefficient is certain situations like determining optimum assignment of jobs to persons, supply of materials from several supply points to several destinations and the like. More effective solution models have been evolved and these are called assignment and transportation models.

The transportation model is concerned with selecting the routes between supply and demand points in order to minimize costs of transportation subject to constraints of supply at any supply point and demand at any demand point. Assume a company has 4 manufacturing plants with different capacity levels, and 5 regional distribution centres. 4 x 5 = 20 routes are possible. Given the transportation costs per load of each of 20 routes between the manufacturing (supply) plants and the regional distribution (demand) centres, and supply and demand constraints, how many loads can be transported through different routes so as to minimize transportation costs? The answer to this question is obtained easily through the transportation algorithm.

Similarly, how are we to assign different jobs to different persons/machines, given cost of job completion for each pair of job machine/person? The objective is minimizing total cost. This is best solved through assignment algorithm.

Uses of Transportation and Assignment Models in Decision Making

The broad purposes of Transportation and Assignment models in LPP are just mentioned above. Now we have just enumerated the different situations where we can make use of these models.

Transportation model is used in the following:

• To decide the transportation of new materials from various centres to different manufacturing plants. In the case of multi-plant company this is highly useful.
• To decide the transportation of finished goods from different manufacturing plants to the different distribution centres. For a multi-plant-multi-market company this is useful.
• To decide the transportation of finished goods from different manufacturing plants to the different distribution centres. For a multi-plant-multi-market company this is useful. These two are the uses of transportation model. The objective is minimizing transportation cost.

Assignment model is used in the following:

• To decide the assignment of jobs to persons/machines, the assignment model is used.
• To decide the route a traveling executive has to adopt (dealing with the order inn which he/she has to visit different places).
• To decide the order in which different activities performed on one and the same facility be taken up.

In the case of transportation model, the supply quantity may be less or more than the demand. Similarly the assignment model, the number of jobs may be equal to, less or more than the number of machines/persons available. In all these cases the simplex method of LPP can be adopted, but transportation and assignment models are more effective, less time consuming and easier than the LPP.

Related posts:

• Operations Research approach of problem solving
• Introduction to Transportation Problem
• Procedure for finding an optimum solution for transportation problem
• Initial Basic Feasible Solution of a Transportation Problem
• Introduction to Decision Models
• Transportation Cost Elements
• Modes of Transportation in Logistics
• Factors Affecting Transportation in Logistics

One thought on “ Transportation and Assignment Models in Operations Research ”

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

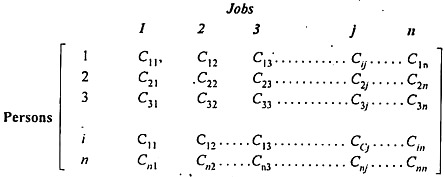
Hungarian Method for Solving Assignment Problem:

The Hungarian method of assignment provides us with an efficient method of finding the optimal solution without having to make a-direct comparison of every solution. It works on the principle of reducing the given cost matrix to a matrix of opportunity costs.

Opportunity cost show the relative penalties associated with assigning resources to an activity as opposed to making the best or least cost assignment. If we can reduce the cost matrix to the extent of having at least one zero in each row and column, it will be possible to make optimal assignment.

The Hungarian method can be summarized in the following steps:

Step 1: Develop the Cost Table from the given Problem:

If the no of rows are not equal to the no of columns and vice versa, a dummy row or dummy column must be added. The assignment cost for dummy cells are always zero.

Step 2:  Find the Opportunity Cost Table:

(a) Locate the smallest element in each row of the given cost table and then subtract that from each element of that row, and

(b) In the reduced matrix obtained from 2 (a) locate the smallest element in each column and then subtract that from each element. Each row and column now have at least one zero value.

Step 3: Make Assignment in the Opportunity Cost Matrix:

The procedure of making assignment is as follows:

(a) Examine rows successively until a row with exactly one unmarked zero is obtained. Make an assignment single zero by making a square around it.

(b) For each zero value that becomes assigned, eliminate (Strike off) all other zeros in the same row and/ or column

(c) Repeat step 3 (a) and 3 (b) for each column also with exactly single zero value all that has not been assigned.

(d) If a row and/or column has two or more unmarked zeros and one cannot be chosen by inspection, then choose the assigned zero cell arbitrarily.

(e) Continue this process until all zeros in row column are either enclosed (Assigned) or struck off (x)

Step 4: Optimality Criterion:

If the member of assigned cells is equal to the numbers of rows column then it is optimal solution. The total cost associated with this solution is obtained by adding original cost figures in the occupied cells.

If a zero cell was chosen arbitrarily in step (3), there exists an alternative optimal solution. But if no optimal solution is found, then go to step (5).

Step 5: Revise the Opportunity Cost Table:

Draw a set of horizontal and vertical lines to cover all the zeros in the revised cost table obtained from step (3), by using the following procedure:

(a) For each row in which no assignment was made, mark a tick (√)

(b) Examine the marked rows. If any zero occurs in those columns, tick the respective rows that contain those assigned zeros.

(c) Repeat this process until no more rows or columns can be marked.

(d) Draw a straight line through each marked column and each unmarked row.

If a no of lines drawn is equal to the no of (or columns) the current solution is the optimal solution, otherwise go to step 6.

Step 6: Develop the New Revised Opportunity Cost Table:

(a) From among the cells not covered by any line, choose the smallest element, call this value K

(b) Subtract K from every element in the cell not covered by line.

(c) Add K to very element in the cell covered by the two lines, i.e., intersection of two lines.

(d) Elements in cells covered by one line remain unchanged.

Step 7:  Repeat Step 3 to 6 Unlit an Optimal Solution is Obtained:

The flow chart of steps in the Hungarian method for solving an assignment problem is shown in following figures:

ADVERTISEMENTS:

Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.

In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.

1. Assignment Model :

Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.

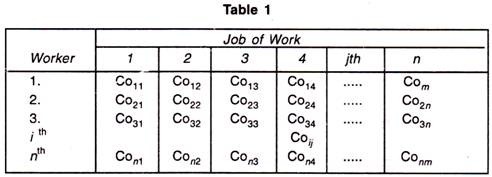
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.

Mathematical Formulation:

Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.

Suppose x jj is a variable which is defined as

1 if the i th job is assigned to j th machine or facility

0 if the i th job is not assigned to j th machine or facility.

Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by

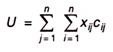
The above definition can be developed into mathematical model as follows:

Determine x ij > 0 (i, j = 1,2, 3…n) in order to

Subjected to constraints

and x ij is either zero or one.

Method to solve Problem (Hungarian Technique):

Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,

1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.

2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.

3. Now, the assignments are made for the reduced table in following manner.

(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.

(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.

(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.

4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:

(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.

(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.

(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.

5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.

6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.

7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.

Related Articles:

• Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
• Linear Programming: Applications, Definitions and Problems

No comments yet.

Leave a reply click here to cancel reply..

You must be logged in to post a comment.