homework & practice 6 1 solve comparison situations

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Multipli. comparison

Multiplicative comparison

Here you will learn about what multiplicative comparisons are and how to use them to solve word problems.

Students will first learn about multiplicative comparisons in 4th grade and expand that knowledge through 5th grade when working with comparison statements and in 6th grade when learning about ratios.

What is multiplicative comparison?

A multiplicative comparison is a way of comparing two quantities by asking how many times larger or smaller one quantity is than the other quantity.

For example, Mary has twice as many cookies as Tim. Tim has 4 cookies. Mary has twice as many balloons as Tim so the number of cookies Mary has = 2 × 4 = 8.

Multiplicative comparisons involve the operations of multiplication and division to solve problems.

A model can help solve multiplicative comparison problems because it helps you to visualize the amounts that need to be compared and to find the unknown quantity.

Let’s look at a few more examples.

Lucas and Ryan are working on a construction project for school. Lucas’s wood board is 5 times the length of Ryan’s board. If Ryan’s wooden board is 3 feet, how long is Lucas’s wooden board?

Draw a bar model to help visualize the situation.

Ryan has a 3 foot board.

From the model, you can see that Lucas’s board is 5 times the length of Ryan’s board. There are 5 groups of 3 feet.

So the equation is 5 \times 3=\text{ length of Lucas's board}

5 \times 3=15

Lucas’s board is 15 feet.

Mike has 3 lollipops. Michelle has 4 times as many lollipops as Mike. How many lollipops does Michelle have?

Draw a picture to model this situation.

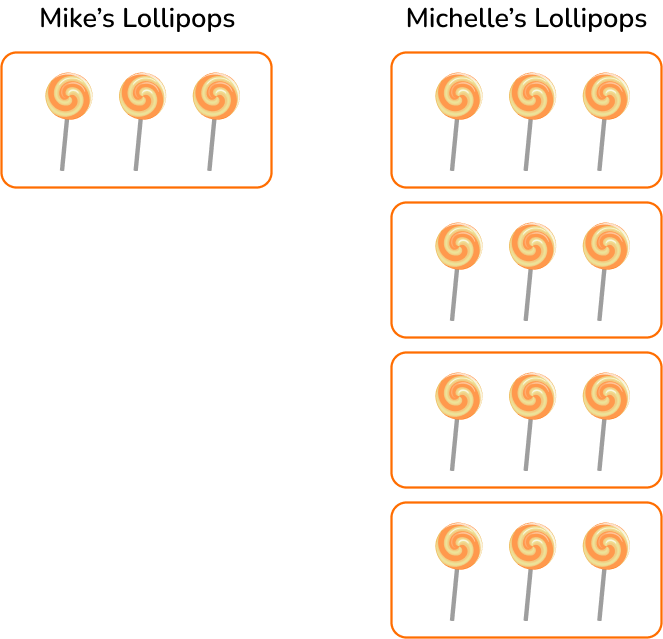
Michelle has four times as many lollipops as Mike. So she has 4 groups of 3 lollipops.

The equation is 4 \times 3=\text { amount of lollipops}

4 \times 3=12

Michelle has 12 lollipops.

Jillian has 12 inches of hair ribbon. Suzanne has half that length. How long is Suzanne’s hair ribbon?

Draw a bar model.

The equation is, \cfrac{1}{2} \, \times 12=\text { length of Suzanne's ribbon}

12 \div 2 = \text { length of Suzanne's ribbon}

12 \div 2=6

Suzanne’s ribbon is 6 inches long.

Common Core State Standards

How does this apply to 4th grade math and 5th grade math?

• Grade 4 – Operations and Algebraic Thinking (4.OA.A.1) Interpret a multiplication equation as a comparison, for example, interpret 35 = 5 \times 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
• Grade 4 – Operations and Algebraic Thinking (4.OA.A.2) Multiply or divide to solve word problems involving multiplicative comparison, for example, by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
• Grade 5 – Number and Operations Base Ten – (5.NBT.B.7) Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.

[FREE] Multiplicative Comparison Worksheet (Grade 4)

Use this worksheet to check your 4th grade students’ understanding of multiplicative comparisons. 15 questions with answers to identify areas of strength and support!

How to solve multiplicative comparison problems

In order to solve multiplicative comparison problems:

Draw a model.

Use multiplication or division to write an equation.

Solve the equation.

Multiplicative comparison examples

Example 1: multiplicative comparison using a bar model with whole numbers.

Maddie has collected 21 stickers. Her friend, Anna, has collected 3 times that amount. How many stickers does Anna have in her collection?

• Draw a model. 

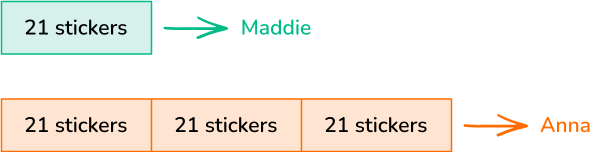
Anna has 3 times the amount of stickers as Maddie. So she has 3 groups of 21.

2 Use multiplication or division to write an equation.

The equation is 3 \times 21= \; ?

3 State the answer.

3 \times 21=63

Anna has 63 stickers.

Example 2: multiplicative comparison using a bar model with whole numbers

Aderonke owns an animal shelter. She has 24 dogs in her shelter and twice as many cats. How many cats are in the shelter?

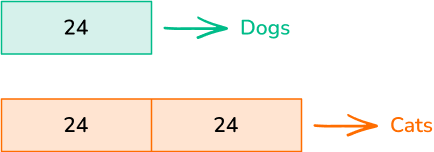
There are twice as many cats as dogs which means there are two groups of 24.

The equation is 2 \times 24= \; ?

2 \times 24=48

Aderonke has 48 cats in her animal shelter.

Example 3: multiplicative comparison using a bar model

Amani has 18 yards of wire. Austin has a third of that length of wire. How much wire does Austin have?

Austin’s wire is a third of the length of Amani’s wire. So, 18 yards is divided into three equal groups.

The equation is 18 \div 3=\text{ length of Austin's wire}

\cfrac{1}{3} \times 18=\text { length of Austin's wire}

\begin{aligned} & 18 \div 3=6 \\\\ & \cfrac{1}{3} \, \times 18=\cfrac{18}{3} \, =6 \end{aligned}

Austin’s wire is 6 yards long.

Example 4: multiplicative comparison using a bar model

Billy saved \$122 dollars. His sister, Nikki, has saved 4 times that amount. How much money has Nikki saved?

Nikki has 4 times the amount of money saved than Billy, which means she has 4 groups of \$122.

The equation is 4 \times 122=\text{ amount of money Nikki saved}

4 \times 122=488

Nikki saved \$488.

Example 5: multiplicative comparison with decimals

Jerome’s neighbor has 92 yards of fencing. Jerome has a fourth of that amount of fencing. How much fencing does Jerome have?

Jerome’s neighbor has 92.4 feet of fencing. He has a fourth of that amount, which means 92.4 is divided into 4 equal groups.

The equation is 92.4 \div 4=\text { length of Jerome's fence}

92.4 \div 4=23.1

Jerome has 23.1 yards of fencing.

Example 6: multiplicative comparison with fractions

Carl has 5 \, \cfrac{1}{2} \, gallons of paint. Lucy has three times that amount.

How many gallons of paint does Lucy have?

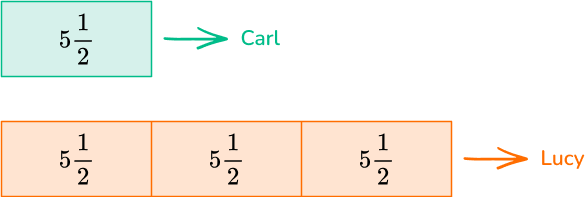
Lucy has three times the amount of gallons of paint than Carl which means there are 3 groups of 5 \, \cfrac{1}{2} .

The equation is 3 \times 5 \cfrac{1}{2}=\text { gallons of paint for Lucy}

\begin{aligned} & 3 \times 5 \, \cfrac{1}{2} \, =3 \times \cfrac{11}{2} \\\\ & 3 \times \cfrac{11}{2} \, =\cfrac{33}{2} \, =16 \cfrac{1}{2} \end{aligned}

Lucy has 16 \, \cfrac{1}{2} \, gallons of paint.

Teaching tips for multiplicative comparison

• Connect visual models to the equations so students can see the visual representation of the abstract equation.
• Math worksheets have their place in a math lesson, but providing students with alternative opportunities to practice such as math games or digital platforms are more engaging.
• Another visual representation that can be used when doing multiplicative comparison word problems is the number line.
• Incorporate projects such as having students create their own multiplicative comparison word problems with answer keys and share them on the Google Classroom.

Easy mistakes to make

• Confusing when to use multiplication versus when to use division For example, when you are given an amount such as 18 and are asked to find 3 times that amount, use multiplication. However, if you are given the amount of 18 and are asked to find a third of that amount, use division.

Related multiplication and division lessons

• Multiplication and division
• Multiplication
• Multiplying and dividing integers
• Multiplying and dividing rational numbers
• Multiplying multi digit numbers
• Dividing multi digit numbers
• Negative times negative
• Long division
• Negative numbers

Practice multiplicative comparison problems

1. Doug has 16 pieces of candy. Dhalia has 3 times that amount. How many pieces of candy does Dhalia have?

Dhalia has 3 times the amount of candy as Doug which means she has 3 groups of 16.

3 \times 16=48

Dhalia has 48 pieces of candy.

2. Danni has 35 pens in her classroom. Jo has 5 times that amount. How many pens does Jo have in her classroom?

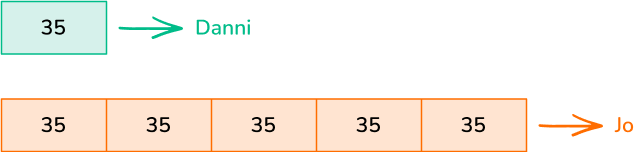
Jo has 5 times as many pens as Danni which means she has 5 groups of 35.

5\times 35=175

Jo has 175 pens in her classroom.

3. Coach Tony has 82 students trying out for his volleyball team. Coach Luke has half that amount trying out for his soccer team. Which equation represents the amount of students trying out for Coach Luke’s soccer team?

Coach Luke has half the number of students trying out for his soccer team than Coach Tony which means 82 is divided into 2 equal groups.

82 \div 2=41

4. Devin has \$243.30 in her savings account. Debra has a third of that amount in her savings account. How much money does Debra have?

Debra has a third of the amount of money as Devin. So \$243.30 has to be divided into 3 equal groups.

243.30 \div 3=81.10

Debra has \$81.10 .

5. Julie has 4 \, \cfrac{2}{3} \, feet of yarn. Dylan has 6 times that amount. How much yarn does Dylan have?

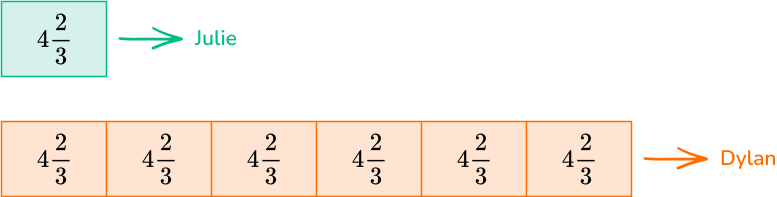
Dylan has 6 times the amount of yarn as Julie, which means 6 groups of 4 \, \cfrac{2}{3} \, .

\begin{aligned} & 6 \times 4 \, \cfrac{2}{3} \, = \\\\ & 6 \times \cfrac{14}{3} \, = \cfrac{84}{3}=28 \end{aligned}

Dylan has 28 feet of yarn.

6. Rory planted a vegetable garden. He planted 51 tomato plants and a third the amount of zucchini plants. How many zucchini plants did he plant?

16 zucchini plants

17 zucchini plants

18 zucchini plants

19 zucchini plants

Rory planted a third of the number of tomato plants which means 51 is divided into 3 equal groups.

51 \div 3=17

\cfrac{1}{3} \, \times 51=17

Multiplicative comparison FAQs

No, you do not always have to write an equation. However, writing equations is a skill necessary for secondary mathematics.

The next lessons are

• Types of numbers
• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

Curriculum  /  Math  /  6th Grade  /  Unit 2: Unit Rates and Percent  /  Lesson 4

Unit Rates and Percent

Lesson 4 of 14

Criteria for Success

Tips for teachers, anchor problems, problem set, target task, additional practice.

Lesson Notes

There was an error generating your document. Please refresh the page and try again.

Generating your document. This may take a few seconds.

Are You Sure?

Are you sure you want to delete this note? This action cannot be undone.

Compare situations using unit rates, including speed, price, and work problems.

Common Core Standards

Core standards.

The core standards covered in this lesson

Ratios and Proportional Relationships

6.RP.A.3.B — Solve unit rate problems including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?

The essential concepts students need to demonstrate or understand to achieve the lesson objective

• Understand that in order to compare two rates, one value must be consistent between the items being compared.
• Use the unit rate as a strategy to compare situations.
• Find and interpret the unit rate to understand what it reveals about a situation.
• Justify choices or decisions between options using sufficient numerical support such as unit rate (MP.3).

Suggestions for teachers to help them teach this lesson

• In terms of pacing, this lesson may need to be extended over more than one day depending on the amount of practice and/or exposure to different variations of problems students need. There are several resources listed in the Problem Set Guidance that can be used for independent or small-group practice. 
• Remind students how they compared situations in Unit 1 using ratio tables and double number lines, finding a common value between the situations and reasoning about the other values.

Lesson Materials

• Calculators (1 per student) — See note from lesson 1.

Unlock features to optimize your prep time, plan engaging lessons, and monitor student progress.

Problems designed to teach key points of the lesson and guiding questions to help draw out student understanding

25-30 minutes

Would you rather buy one 5-pound jug of honey for $15.35, or three 1.5-pound bottles of honey for $14.39? Justify your answer. 

Guiding Questions

Student response.

Upgrade to Fishtank Plus to view Sample Response.

Would You Rather 48 by John Stevens is made available on  Would You Rather  under a  CC BY-NC 4.0  license. Accessed on Jan. 17, 2019, 11:12 a.m..

Yaritza and Eddy race to school on their bikes. Eddy bikes 2 miles in 12 minutes, and Yaritza bikes 3 miles in 15 minutes. Who is going faster?

A set of suggested resources or problem types that teachers can turn into a problem set

15-20 minutes

Give your students more opportunities to practice the skills in this lesson with a downloadable problem set aligned to the daily objective.

A task that represents the peak thinking of the lesson - mastery will indicate whether or not objective was achieved

5-10 minutes

Jack and Priya are setting up folding chairs for their school’s weekly Community Meeting. Jack can unfold and set up 55 chairs in 20 minutes. Priya can unfold and set up 44 chairs in 15 minutes. Who works at the faster rate? Justify your answer.

The following resources include problems and activities aligned to the objective of the lesson that can be used for additional practice or to create your own problem set.

• EngageNY Mathematics Grade 6 Mathematics > Module 1 > Topic C > Lesson 23 — Examples and Problem Set
• EngageNY Mathematics Grade 6 Mathematics > Module 1 > Topic C > Lesson 16 — Problem Set
• EngageNY Mathematics Grade 6 Mathematics > Module 1 > Topic C > Lesson 20 — Exploratory Challenge and Problem Set; Do not include problems that have equations or coordinate planes, as those have not yet been covered.
• Illustrative Mathematics Ticket Booth
• Inside Mathematics Problems of the Month First Rate
• Yummy Math How Much Does a Lego Cost?
• Robert Kaplinsky Which Carrots Should You Buy?
• Open Up Resources Grade 6 Unit 3 Lesson 2

Solve challenging problems involving unit rate.

Topic A: Defining Rate & Solving Rate Problems

Investigate and use rate in real-world situations.

6.RP.A.3 6.RP.A.3.B

Define rate and unit rate, and find rates from situations involving ratios.

6.RP.A.2 6.RP.A.3.B

Find unit rates and use them to solve problems.

6.RP.A.2 6.RP.A.3 6.RP.A.3.B

Create a free account to access thousands of lesson plans.

Already have an account? Sign In

Topic B: Measurement Unit Conversions

Reason with measurement units and solve unit conversion problems using different strategies.

Solve measurement unit conversion problems.

Topic C: Percent

Define percent as a rate per 100. Find percentages of 100 and 1.

Solve percent problems using benchmark fractions and percentages, with and without written work.

Convert between fractions, percent, and decimals.

Find a percent of a quantity.

Find the whole quantity, given a part and percent.

Solve percent problems, including finding percent when given a part and a whole.

Solve multi-step problems involving rate and percent.

6.RP.A.2 6.RP.A.3 6.RP.A.3.C 6.RP.A.3.D

Request a Demo

See all of the features of Fishtank in action and begin the conversation about adoption.

Learn more about Fishtank Learning School Adoption.

Contact Information

School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.

We Handle Materials So You Can Focus on Students

We've got you covered with rigorous, relevant, and adaptable math lesson plans for free

Comparison Word Problems

Related Pages Comparing & Ordering Numbers Comparing Numbers Worksheet More Word Problems Algebra Word Problems

In these lessons, we will learn how to solve comparison word problems using either bar models or comparison bars.

Printable Word Problem Worksheets for 1st Grade: Addition Word Problems Addition/Subtraction Word Problems Comparison Word Problems

The following diagrams show the three types of comparison word problems: Difference Unknown, Unknown Big Quantity, Unknown Small Quantity. Scroll down the page for examples and solutions.

Types of Comparison Word Problems

There are three main types of comparison word problems.

Difference Unknown Connie has 15 red marbles and 28 blue marbles. How many more blue marbles than red marbles does Connie have? This is a subtraction problem. 28 - 15 = 13

Unknown Big Quantity Connie has 15 red marbles and some blue marbles. She has 13 more blue marbles than red ones. How many blue marbles does Connie have? This is an addition problem. 15 + 13 = 28

Unknown Small Quantity Connie has 28 blue marbles. She has 13 more blue marbles than red ones. How many red marbles does Connie have? This is a subtraction problem. 28 -13 = 15

How to solve comparison word problems using Bar Models or Tape Diagrams?

This video explains how to use bar modeling in Singapore math to solve word problems that deal with comparing. This technique of using model drawings to solve word problems is recommended by the Common Core mathematics standards.

Example: Adam has 11 fewer lollipops than Hope. If Adam has 16 lollipops, how may lollipops does Hope have?

Bar Model (Comparison) This video employs a visual way to solve world problems using bar modeling. This type of word problem uses the comparison model. Because the part is missing, this is a subtraction problem.

Example: Cayla did 88 sit-ups in the morning. Nekira did 32 sit-ups at night. How many more sit-ups did Cayla do than Nekira?

How to solve comparison word problems using Comparison Bars?

This is another strategy that we can use for story problems that involves comparison.

• Bob has 14 crackers. Steve ate five fewer than Bob. How many did Steve eat?
• David has 5 marbles. Anna has 8 marbles. How many more does Anna have than David?
• Ellie has 9 goldfish. Laney has 5 more goldfish than Ellie. How many goldfish does Laney have?
• Mark earned $428 doing yard work. Troy earned $186. How much less did Troy earn?
• Billy has 679 gumballs. He has 278 more gumballs than Lee. How many gumballs does Lee have?
• Jake has 219 bottlecaps. Then, he found some more. Now he has 347 bottlecaps. How many bottlecaps did he find?

Comparison Bars

• Claire has 8 marbles. Sasha has 15 marbles. How many more marbles does Sasha have than Claire?
• Bill read 5 books. Beth read 2 more books than Bill. How many books did Beth read?
• Beth read 8 books. Bill read 3 fewer books than Beth. How many books did Bill read?

Example: The Nature Center has a collection of snakes. The redbelly snake in the collection is 9 inches long. The eastern ribbon snake is 21 inches long. How much longer is the eastern ribbon snake than the redbelly snake?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

6.1.1A Locate & Compare Numbers

Standard 6.1.1.

Locate positive rational numbers on a number line and plot pairs of positive rational numbers on a coordinate grid.

Compare positive rational numbers represented in various forms. Use the symbols  < ,  =  and  >.

For example : $\frac{1}{2}$ > 0.36.

Standard 6.1.1 Essential Understandings

Relationships of equivalence with different forms of rational numbers can be illustrated in a variety of representations. Students use fractions, decimals, and percents to describe equivalent positive rational numbers. Clement (2004) suggests five different kinds of representations for teaching students the concepts of fractions, decimals and percents. These five representations are pictures, manipulatives, spoken language, written symbols, and relevant situations. Conceptual understanding of these equivalencies is developed as students describe these rational numbers in concrete representational forms (fraction strips, Cuisenaire rods, pattern blocks, etc.); visual representational forms (grids, diagrams, pictures, etc.); and abstract symbolic form. Using these same structures, students expand their understanding of equivalence with rational numbers to making comparisons between them. Students' learning experiences with these different forms of representation guide them in identifying and selecting appropriate forms for making comparisons and conversions in a particular situation.

The skills of prime factorization, least common multiple, and greatest common factor become tools for students in their formation of equivalent fractional numbers. Student understanding of representing whole numbers as a product of factors with exponents is aided by their previous work with whole numbers, multiples, factors and exponents.

 All Standard Benchmarks

●      6.1.1.1 Locate positive rational numbers on a number line and plot pairs of positive rational numbers on a coordinate grid.

●      6.1.1.2 Compare positive rational numbers represented in various forms. Use the symbols <, =, and >.

●      6.1.1.3 Understand that percent represents parts out of 100 and ratios to 100.

●      6.1.1.4 Determine equivalences among fractions, decimals, and percents: select among these representations to solve problems.

●      6.1.1.5 Factor whole numbers; express a whole number as a product of prime factors with exponents.

●      6.1.1.6 Determine greatest common factors and least common multiples. Use common factors and common multiples to calculate with fractions and find equivalent fractions.

●      6.1.1.7 Convert between equivalent representations of positive rational numbers.

Benchmark Group A

• 6.1.1.1 Locate positive rational numbers on a number line and plot pairs of positive rational numbers on a coordinate grid.
• 6.1.1.2 Compare positive rational numbers represented in various forms. Use the symbols <, =, and >.

 What students should know and be able to do [at a mastery level] related to these benchmarks.

  ●      Use a number line to locate and compare rational numbers, including fractions, decimals, and percents;

●      Convert between fractions, decimals, and percents;

●      Represent the relationship between two positive rational numbers using <, =, or >;

●      Identify the origin, horizontal (x), and vertical (y) axes on a coordinate grid;

●      Plot ordered pairs of rational numbers on a coordinate grid.

Work from previous grades that supports this new learning includes:

●      Read and write decimals using place value to describe decimals in terms of groups from millionths to millions; recognize the numbers to the left are less than the numbers to the right on a number line;

●      Find 0.1 more than a number and 0.1 less than a number.  Find 0.01 more than a number and 0.01 less than a number.  Find 0.001 more than a number a 0.001 less than a number;

●      Order fractions and decimals, including mixed numbers and improper fractions, and locate on a number line;

●      Recognize and generate equivalent decimals, fractions, mixed numbers and improper fractions in various contexts;

●      Round numbers to the nearest 0.1, 0.01, and 0.001;

●      Use a rule or table to represent ordered pairs of positive integers and graph these ordered pairs on a coordinate system.

NCTM Standards

  Understand numbers, ways of representing numbers, relationships among numbers, and number systems

• work flexibly with fractions, decimals, and percents to solve problems;
• compare and order fractions, decimals, and percents efficiently and find their approximate locations on a number line;
• develop meaning for percents greater than 100 and less than 1;
• understand and use ratios and proportions to represent quantitative relationships;
• use factors, multiples, prime factorization, and relatively prime numbers to solve problems.

Common Core State Standards

4NF (NUMBER AND OPERATIONS -  FRACTIONS) Extend understanding of fraction equivalence and ordering.

• 4NF.7 Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.

4OA. (OPERATIONS AND ALGEBRAIC THINKING) Gain familiarity with factors and multiples.

• 4OA.4 Find all factor pairs for a whole number in the range 1-100. Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range 1-100 is a multiple of a given one-digit number. Determine whether a given whole number in the range 1-100 is prime or composite.

5NBT (NUMBER AND OPERATIONS IN BASE TEN) Understand the place value system.

• 5NBT.3b Compare two decimals to thousandths based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons.

6NS (NUMBER SYSTEM) Apply and extend previous understandings of multiplication and division to divide fractions by fractions.

• 6NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor.
• 6NS.6 Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
• Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., -(-3) = 3, and that 0 is its own opposite.
• Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
• Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
• 6NS.7 Understand ordering and absolute value of rational numbers.
• 6NS.7.b Write, interpret, and explain statements of order for rational numbers in real-world contexts. For example, write -3 0 C > -7 0 C to express the fact that -3 0 C is warmer than -7 0 C.

6RP (RATIOS AND PROPORTIONAL RELATIONSHIPS) Understand ratio concepts and use ratio reasoning to solve problems.

• 6RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
• 6RP3.c Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.

Misconceptions

Student Misconceptions and Common Errors

• When partitioning a whole on a number line to locate fractional parts, students may count partition marks rather than pieces resulting in an answer of fifths rather than sixths; or count the beginning and end marks, resulting in sevenths rather than sixths.
• When comparing fractions, students may focus only on the size of the denominator.

Example : $\frac{3}{8}$ is NOT larger than $\frac{3}{4}$ even though the number 8 is larger than the number 4.

• Overgeneralizing can be a problem when comparing same size of fraction with differing sized wholes.

Example:  $\frac{1}{4}$ cup as compared to $\frac{1}{4}$ gallon

• When comparing decimals, students may not have an understanding of place value to the right of the decimal point. Example: Students may believe that 5.155 is greater than 5.3 because there are more digits.
• Students may believe that adding "0" to the end of a decimal makes it 10 times larger, since 530 is 10 times larger than 53.When considering adding a "0" to the end of a whole number, the value changes. Students sometimes do not recognize that value of a decimal does not change when a "0" is added to the end of a decimal.
• Students confuse the symbols for "less than" and "greater than;"
• Students may not understand the order of the coordinates when locating points on a coordinate grid;
• Students struggle identifying the coordinates of points located on the horizontal or vertical axes.

In the Classroom

In this vignette, students discover a mystery word by graphing ordered pairs on a coordinate grid.

Teacher:   At your desks, each of you has a piece of graph paper and a set of directions that will lead you to discover a mystery word .  It's important to follow the directions carefully. Sometimes you'll be asked to connect the points in order and sometimes the points will not get connected. 

Directions:

Use your graph paper to draw a coordinate grid.  Clearly label the x- and y- axes.

Plot the following ordered pairs and connect them in the order given.

Start (8, 3), (8, -3) Stop

Start (13, 3), (13, -3) Stop

Start (8, 0), (13, 0) Stop

Start (-6, 3), (-6, 0), (-3.5, 3), (-1, 0), (-1, -3) Stop

Start (-1, 0), (-6, 0) Stop

Start (1, 3), (6, 3) Stop

Start (3.5, -3), (3.5, 3) Stop

Start (-13, -3), (-13, 3), (-10.5, 0), (-8, 3), (-8, -3) Stop

Teacher: Let's do the first step together. The directions say, "Start (8, 3), (8, -3) Stop." What do you think that means?

Student: I think it means to start by graphing a point at (8, 3), then draw a line to connect that point to a point at (8, -3), and then stop.

Teacher: So how do you know where to graph the point (8, 3)? Student: Well, you start at the origin, move 8 units to the right, then up 3 units and plot the point.

Teacher: Tell me about the 'origin'.

Student: The origin is the point at (0, 0). It's the place where you always start when you locate points.

Teacher: That makes sense, because 'origin' means starting point. Why do you think the origin (0, 0), has two numbers?

Student: All points on the coordinate grid have two numbers. They're an ordered pair.

Teacher: Why did you describe the numbers as an 'ordered' pair?

Student: Because the order of the two numbers matters. The first number tells you how far to move right or left, and the second number tells you how far to move up or down.

Teacher: So what happens if you move up or down first, then move left or right?

Student: You end up in a different place.

Teacher: Show me an example.

Student: Sure. Here's where (8, 3) and (3, 8) are located.

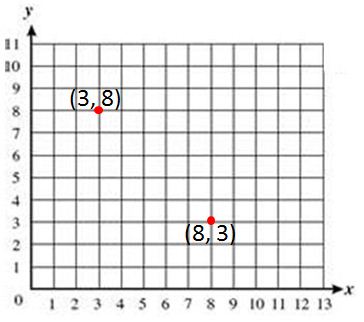
Teacher: We can see that reversing the order of the numbers results in a different location, so the order certainly matters. It's very important to know that the first number tells you how far to move left or right, and the second number tells how far to move up or down. What strategies do you use to help you remember that?

Student: I think about the coordinate axes as two number lines - one horizontal and the other vertical. In elementary school, we often used horizontal number lines. We used them to learn about all sorts of things, like adding, subtracting, multiplying, and dividing. I think about learning math when I was younger and that helps me remember to begin with the horizontal number line and move right or left first.

Student: I have another way to remember the order. My teacher last year told me to think of a ladder. You must walk to the ladder first and then go up or down.

Teacher: Those are two good strategies. Thank you for sharing. Yes, the coordinate axes are really two number lines that intersect at right angles. We refer to the horizontal axis as the x -axis and the vertical axis as the y -axis. The origin (0, 0), is the point where the two axes intersect.

Student: I use another strategy to help me remember the order of the numbers.

Teacher: What's that?

Student: Well, the ordered pair is in alphabetical order. First is the x -coordinate, then the y -coordinate. The x -coordinate tells you how far to move on the x -axis and the y -coordinate tells you how far to move on the y -axis.  I draw an imaginary line at those two places, and I know that the place where those lines intersect is where the point is located.

Teacher: Show us how you would use that strategy to locate (8, 3).

Student: Like this.

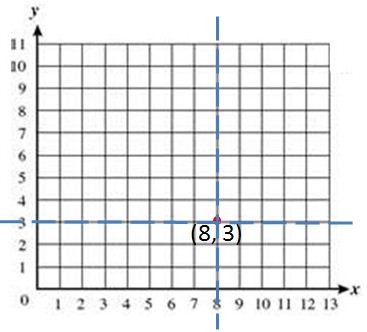
Teacher: That's the same location as we found using the other strategy. How do you remember that the horizontal axis is the x- axis and the vertical axis is the y -axis?

Student: Easy. I think about drawing an outdoor picture. I would start by drawing the horizon, or horizontal axis. Because the ordered pair is in alphabetical order and x comes before y, I know that the horizontal axis is the x -axis. Then the vertical axis must be the y- axis.

Teacher: Clever. Sounds like you have some strategies to help you discover the mystery word .  Go ahead and begin your investigation.

(Students discover the Mystery Word is "MATH.")

Student:   "Math" isn't much of a mystery word in math class.

Teacher:  Good point. Perhaps you have other ideas for words that could be used as mystery words.  That can be tomorrow's homework assignment.  I want each of you to choose a Mystery Word and write the directions necessary to discover it using a coordinate grid.  Tomorrow you'll be given time in class for your partners to discover your Mystery Word.

Teacher Notes

• Determining whether a student understands partitioning a whole on a number line can be assessed informally by observation. When misconceptions are observed, it is helpful to highlight divided sections to aid in the correct identification of numbered parts.
• Many students understand $\frac{4}{5}$ to be "4 parts out of 5." These students are confused when they encounter $\frac{7}{5}$ as they do not understand how you can have "7 parts out of 5." Be aware of the language used when talking about fractions. Emphasize the relationship as part-to-whole, rather than part "out of" whole. Students can visualize $\frac{7}{5}$ when they think of having 7 leftover brownies, with a whole pan being cut into 5 parts.
• Comparisons among fractions with different denominators are difficult for most students. Draw pictures with students to visualize the fractions. For situations when the pictures aren't sufficient to make comparisons, emphasize the need to have the whole cut into the same number of parts and find equivalents;
• Instead of always encouraging students to simplify every time, remind students to look for the equivalent form that best expresses what they want or need to say.
• Students will need a classroom "museum" filled with opportunities to work with specific fractions of various sizes.

Example:  $\frac{1}{4}$ cup and $\frac{1}{4}$ gallon vary greatly in size even though both use the measure of $\frac{1}{4}$.

• It will be helpful to review converting between equivalent representations of rational numbers before asking students to make comparisons between fractions, decimals, and percents.
• Demonstration of the addition of a "0" to both a whole number and a decimal number may need to be given. For example: If we add a "0" to the back of 54, we have 540; but, if we add a "0" to the end of 5.4 to make 5.40, we still have 5.4 as a value.
• A quick review with the symbols used for comparing numbers may be needed as a refresher for students.
• Students may try to round numbers that have repeating decimals and incorrectly order the numbers. Remind them that even though you often round repeating decimals, the decimal is actually less than or greater than the rounded decimal.

Example: $0.\bar{3}$ is greater than 0.3 and less than 0.33.

• When asking students to plot points on a coordinate grid, it will be helpful to refer to the coordinates as ordered pairs , to help students make the connection that order matters.
• Finding Your Way Around

Students practice naming and graphing ordered pairs, and use the coordinate plane to create geometric figures.

• Equivalent Fractions

Students create equivalent fractions by dividing and shading squares or circles, and match each fraction to its location on the number line.

• Plotting Points on a Coordinate System

Author: Francine Nettesheim

2009© Wisc-Online.com

Students use a coordinate grid to plot points in all four quadrants.

• Fraction Models

Students explore different representations for fractions, including improper fractions, mixed numbers, decimals, and percents.

• Fraction Game

This applet allows students to work with relationships among fractions and ways of combining fractions.

 Additional Instructional Resources

• " 10 Practical Tips for Making Fractions Come Alive and Make Sense ." National Council of Teachers of Mathematics . Web. 20 Feb. 2011. 

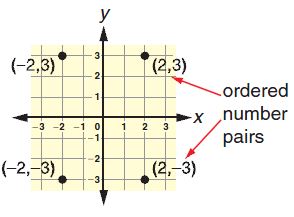
coordinate grid: a grid for locating points in a plane by using ordered pairs of numbers. It is formed by two number lines that intersect at right angles at their zero points. Example:

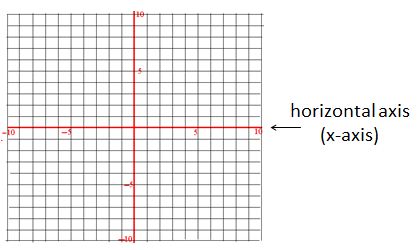
horizontal axis: positioned in a left-to-right position, parallel to the line of the horizon; referred to as the x-axis.  Example:

integers: a number in the set {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}.  All integers are rational numbers, but not all rational numbers are integers.  Example: $-\frac{1}{4}$ is a rational number but not an integer.) 

            All whole numbers are integers, but not all integers are whole numbers. 

            Example: -2 is an integer, but not a whole number.)

            Examples: 3 and -3

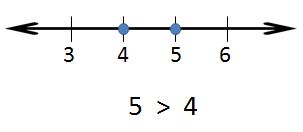
 is greater than (>): a number "is greater than" another number if its value is larger than the compared number.  When two numbers are plotted on the number line, the number with the larger value will be on the right .   Example:

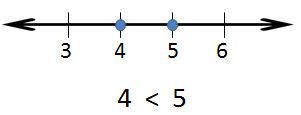
is less than (<): a number "is less than" another number if its value is smaller than the compared number.  When two numbers are plotted on the number line, the number with the smaller value will be on the left .   Example:

ordered pair (x,y): a pair of numbers used to locate a point on a coordinate grid.  The first number corresponds to a position along the horizontal ( x ) axis, and the second number corresponds to a position along the vertical ( y ) axis.  Example:

per: for each, or for every .  Example:   If apples cost $1.99 per pound, then each pound of apples costs $1.99.

percent (%):   per hundred, or out of 100

Example:  "12% of sixth grade students are left-handed" means that out every 100 sixth grade students, 12 are left-handed.

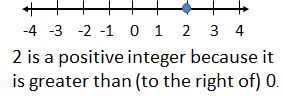
ratio:   comparison of two quantities by division.  This relationship can be expressed as a fraction, decimal, or percent, as well as with a colon or in words. Note: Fractions can be used to express both part-to-part and part-to-whole relationships. It is recommended to avoid writing part-to-part relationships as $\frac{a}{b}$ to avoid confusion with part-to-whole relationships. Example:   If a team wins 3 games out of 5 games played, the ratio of wins to total games played can be written as $\frac{3}{5}$ , 0.6, 60%, 3 to 5, 3:5  or "three to five."

rational number: any number that can be expressed in the form $\frac{a}{b}$ where a and b are integers and b≠0.   A rational number can always be represented by either a terminating or a repeating decimal.  Examples:   $\frac{2}{3}$, 4 (which can be expressed as $\frac{4}{1}$);  2.25 (which can be expressed as $\frac{225}{100}$).

simplify (fraction): to express in simplest form, or lowest terms.  The numerator and denominator of proper fractions in simplest form have no common factor other than 1. Improper fractions and mixed numbers are in simplest form when the fraction part is proper and in simplest form.  Examples: The numerator and denominator of  $\frac{4}{8}$ share the common factor 4, so must be rewritten as $\frac{1}{2}$ to be in simplest form ; $\frac{10}{4}$ written in simplest form is  $\frac{5}{2}$ or $2\frac{1}{2}$.

x-axis: the horizontal number line in the coordinate plane .  Example:

vertical axis: the vertical number line in the coordinate plane.  Example:

 y-axis: the vertical axis .  Example:

Reflection - Critical questions regarding the teaching and learning of these benchmarks

• Beyond procedural knowledge, what does a student need to understand about place value and the number system to make conversions?
• How can we help students compare numbers when they struggle to translate among fractions, decimals, and percents?
• How can we reinforce the relationship among decimals, percents, and fractions?
• How can we connect locating points on a number line to locating pairs of points on the coordinate grid?
• What connections can be made to real life to motivate students?
• Cramer, K., Behr, M., Post T., Lesh, R. (2009). The Rational Number Project   (choose RNP: Initial Fraction Ideas)The Rational Number Project (RNP) advocates teaching fractions using a model that emphasizes multiple representations and connections among different representations.
• Behr, M. & Post, T. (1992). Teaching rational number and decimal concepts .  In T. Post (Ed.), Teaching mathematics in grades K-8: Research-based methods (2nd ed.) (pp. 201-248). Boston: Allyn and Bacon.  
• Clarke, D. M., Roche, A., & Mitchell, A. Ten practical tips for making fractions come alive and make sense. Article discusses key ideas and concepts involved in understanding fractions and offers a range of hints to the classroom teacher on how to support students to develop a connected understanding of this important topic. Includes a fractions activity sheet. Located at:

Clement, L. L. (2004). A model for understanding, using, and connecting representations. Teaching children mathematics, 11 (2) , 97 - 102.

Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study . Thousand Oaks, CA: Corwin Press.

Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.

Mathematics Curriculum Framework. (2000). Malden, MA: Massachusetts Department of Education.

Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN:  SciMathMN.

Mathematics Framework for the 2009 National Assessment of Educational Progress. (2009).   Washington, D.C.: National Assessment Governing Board U.S. Department of Education.

Mathematics 6-8 GaDOE: Georgia Department of Education , n.d. Web. 29 Mar. 2011.

Cramer, K., Behr, M., Post T., Lesh, R. (2009). The Rational Number Project    (choose RNP: Initial Fraction Ideas) The Rational Number Project (RNP) advocates teaching fractions using a model that emphasizes multiple representations and connections among different representations.

Behr, M., & Post, T. (1992). Teaching rational number and decimal concepts .  In T. Post (Ed.), Teaching mathematics in grades K-8: Research-based methods (2nd ed.) (pp. 201-248). Boston: Allyn and Bacon.

(DOK: Level 1)

1.      Find the value of x . 

2.      Place the ordered pairs on the coordinate grid shown below.

(9, 0)                      (2, 6)                (8, 5)                (0, 7)

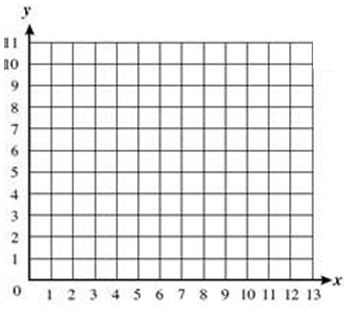
(DOK: Level 2)

3..      Place each of the numbers on the number line shown below.

  $1\frac{1}{4}$                  0.7                   2.3                   $\frac{3}{2}$

4.      Tell whether the following statements are true or false.

____ a. $\frac{3}{5} < 0.6$

____ b. $0.3 = 0.33$

____ c. $\frac{2}{3} > \frac{2}{5}$

____ d. $5.4 < \frac{5}{4}$

____ e. $\frac{2}{5} > 25%$

_ F __ a. $\frac{3}{5} < 0.6$

_ F __ b. $0.3 = 0.33$

_ T __ c.  $\frac{2}{3} > \frac{2}{5}$

_ F __ d. $5.4 < \frac{5}{4}$

_ F __ e. $\frac{2}{5} > 25%$

(DOK: Level 3)

5.      Marta and Jeff each ordered pizzas - the same size pizza.  Marta cut her pizza into 6 pieces, and ate 3 pieces.  Jeff cut his pizza into 7 pieces and also ate 3 pieces.  Who ate more pizza?  Explain how you know.

Sample Answer:  Marta ate more pizza.  Although Marta and Jeff both ate 3 pieces of pizza, each of Jeff's pieces were smaller since he cut his pizza into 7 pieces rather than 6.

6.      Reaching the Goal:  The goal of a community fundraiser was to earn $10,000.  The picture below shows the results after one week.  What part of the goal was reached after one week?  Express your answer as a fraction, decimal, and percent.  Explain how you found your answers.

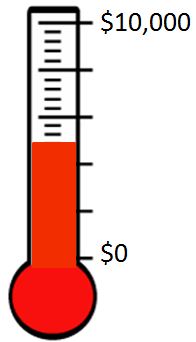
Sample Answer:  $\frac{12}{25}$; 0.48, or 48%; there are 5 pieces between 0 and 10,000 and each piece is broken into 5 parts.  Since 5 x 5 = 25, there are 25 parts total parts.  The thermometer shows that 12 of the 25 are colored in. To find a decimal, the denominator needs to be a power of 10.  Multiplying $\frac{12}{25}$  by $\frac{4}{4}$ or 1, tells me that $\frac{48}{100}$ has the same value. $\frac{48}{100}$ written as a decimal is 0.48.  Since percent means out of 100, that is the same as 48%.

(DOK Level 4)

A)     Identify three numbers between 0.5 and 0.6. Express one as a decimal, one as a fraction, and one as a percent.

B)     Locate and label the numbers on the number line shown below.

C)     Write an expression using < to show their relationship.

D)     Tell how you could make the smallest number equivalent to the largest number.

Sample Answers:

A)  0.52, 57%, $\frac{59}{100}$

C)  0.52 < 57% < $\frac{59}{100}$

D)  Adding 0.07 to 0.52 results in 0.59, which is equivalent to $\frac{59}{100}$.

Differentiation

Struggling Students

●      Provide constant use of the number line to make comparisons. Remind students that values increase as you move to the right. Include decimal and percent equivalencies for benchmarks.

●      Create a fraction "tool-kit." Have several strips that represent candy bars cut to the same dimensions. Spend several days folding the candy bars to represent common fraction denominators such as fourths, eighths, halves, thirds, sixths, twelfths, fifths, and tenths. Ask students to "compare" or "show" various fractions.   Example: " Which would you rather have? 3 fifths of a candy bar or 5 sevenths of a candy bar?"

●      Provide a rich and varied supply of manipulatives and tools such as geoboards, 100 grids, base-ten blocks, and number lines to represent rational numbers and make comparisons.  Example: Base-100 blocks can be used to compare 0.23 and 0.17, or geoboards can be used to compare $\frac{1}{4}$ to $\frac{3}{8}$.

• Review fraction equivalency concepts before connecting to decimals or percents.

• To prevent misconceptions and increase the understanding of decimals, fractions, and percents among special education students, it may help to develop students' understanding of rational numbers through percents first. Research suggests that humans easily see objects in proportional terms (full, half full, nearly empty, etc.) Students can estimate the "fullness" of beakers filled with water by assigning a numerical value from 1 to 100. Frequent exposure to percents can strengthen equivalency comprehension. Another benefit of beginning with percents is that every percentage has a corresponding fractional or decimal equivalent that is simple to determine. For example, 77% can easily be written as $\frac{77}{100}$ or 0.77. This conversion process is effortless and allows students to develop their own procedures rather than memorizing algorithms.
• Provide pocket-sized fact charts to aid in equivalency.
• Have students verbalize as they translate from one form to another.
• Help students see relevancy of fractions, decimals, and percents by using real-world examples; e.g. discounts, sports statistics, sales tax.
• Connect learning to real-world experiences. Example: Library materials are organized using the Dewey decimal system. To locate a book numbered 392.134, they need to understand that it comes between 392.13 and 392. 14, even though it appears "longer."
• Commas and periods are used differently to denote place value in other countries. Example, 2,3141.5 in the United States is written as 2.341,5 in some South American countries. For these students, it is necessary to explicitly connect their prior experiences of notation to notation in the United States.
• Use fractional language when describing decimals. Example: Read 2.75 as "2 and 75 hundredths" rather than "2 point 75." This reinforces place value and helps build a more conceptual understanding of decimals.
• Encourage Think-Alouds. Example : Partner up an ELL student with another student with good English language skills to explain his/ her thinking.
• Identify that the fraction $\frac{1}{4}$ can have many meanings. For example:
• A part of a whole: $\frac{1}{4}$ of a pizza;
• A part of a collection: $\frac{1}{4}$ of a group of students;
• A measurement: $\frac{1}{4}$ of a mile;
• A probability: 1 chance in 4;
• A number: the number halfway between 0 and $\frac{1}{2}$
• A division: ${1}\div{4}$

●      Make vocabulary connections explicit in your teaching. Example : In addition to identifying the denominator as the "number on the bottom," include that the denominator represents the number of equal-sized pieces into which the whole is cut.

• Provide a picture dictionary.
• Use graphic organizers such as the Frayer model shown below, for vocabulary development.

    Ask students to use a city map (or create their own coordinate grid) to communicate their path to school using given map coordinates. Have students play chess and record their moves using chess notation.

Chess Notation : This website can be used as a resource for teachers who are interested in teaching chess notation.

Example: Ng1tof3 means moving the Knight from space g1 to space f3.

• Chesskids This website provides a tutorial for learning about chess.

●      Have students create a deck of cards with fractions, decimals, and percents that can be used to play " War ," a game where two players battle by comparing two cards and the player with the card showing the larger value "wins" the battle and takes the "loser's" card.  When the cards show equivalencies, the battle continues until a winner is declared.

●      Students can create pairs of cards showing unfamiliar equivalencies and use them to play Concentration , a memory game. Negative rational numbers could be included as a challenge.

Parents/Admin

Administrative/Peer Classroom Observation

Parent Resources

• Billy Bug and His Quest for Grub

This interactive website provides practice for locating points on a coordinate grid.

• Decimals - and - Percents

This website provides brief written instructions, a video tutorial, practice problems, and a quick quiz on converting fractions to decimals and percents.

• Fraction Frenzy

Students identify equivalent fractions through various levels of difficulty to win points.

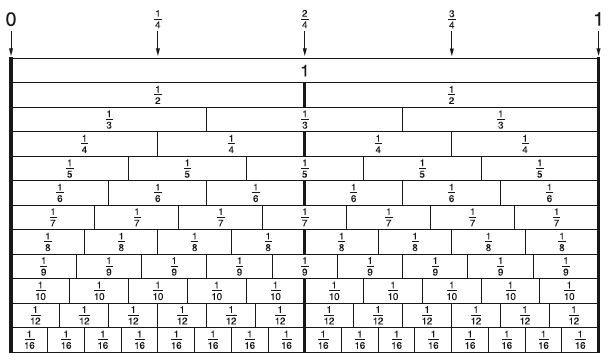
• Ordering Dominoes

Use dominoes to represent fractions, as shown in the example below. Ask students to put 5 dominoes in ascending order and justify the order.  A calculator may be helpful for converting fractions

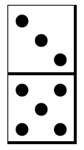
• Students are asked to order 5 dominoes in ascending order and justify the order. Sample dominoes that work well when teaching basic equivalency include: $\frac{1}{3}, \frac{2}{5}, \frac{3}{5}, \frac{2}{4}, \frac{2}{3}, \frac{1}{4}, \frac{1}{5}$.

Related Frameworks

• 6.1.1.1 Number Line & Coordinate Grid
• 6.1.1.2 Compare Numbers

6.1.1B Equivalence & Representations

• 6.1.1.3 Percents
• 6.1.1.4 Fractions, Decimals, Percents: Equivalence
• 6.1.1.7 Positive Rational Numbers: Equivalent Representations

6.1.1C Factors & Primes / GCF & LCM

• 6.1.1.5 Factors & Prime Factors
• 6.1.1.6 Common Factors & Common Multiples