assignment problem max flow

• Interview Problems on Graph
• Practice Graph
• MCQs on Graph
• Graph Tutorial
• Graph Representation
• Graph Properties
• Types of Graphs
• Graph Applications
• BFS on Graph
• DFS on Graph
• Graph VS Tree
• Transpose Graph
• Dijkstra's Algorithm
• Minimum Spanning Tree
• Prim’s Algorithm
• Topological Sorting
• Floyd Warshall Algorithm
• Strongly Connected Components
• Advantages & Disadvantages

Ford-Fulkerson Algorithm for Maximum Flow Problem

The Ford-Fulkerson algorithm is a widely used algorithm to solve the maximum flow problem in a flow network. The maximum flow problem involves determining the maximum amount of flow that can be sent from a source vertex to a sink vertex in a directed weighted graph, subject to capacity constraints on the edges.

The algorithm works by iteratively finding an augmenting path, which is a path from the source to the sink in the residual graph, i.e., the graph obtained by subtracting the current flow from the capacity of each edge. The algorithm then increases the flow along this path by the maximum possible amount, which is the minimum capacity of the edges along the path.

Given a graph which represents a flow network where every edge has a capacity. Also, given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with the following constraints:

• Flow on an edge doesn’t exceed the given capacity of the edge.
• Incoming flow is equal to outgoing flow for every vertex except s and t.

For example, consider the following graph from the CLRS book. 

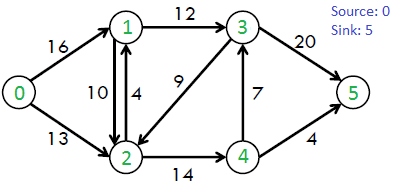
The maximum possible flow in the above graph is 23. 

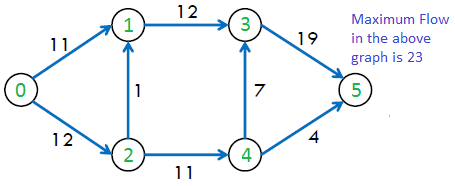
Prerequisite : Max Flow Problem Introduction

Ford-Fulkerson Algorithm    The following is simple idea of Ford-Fulkerson algorithm: Start with initial flow as 0. While there exists an augmenting path from the source to the sink:   Find an augmenting path using any path-finding algorithm, such as breadth-first search or depth-first search. Determine the amount of flow that can be sent along the augmenting path, which is the minimum residual capacity along the edges of the path. Increase the flow along the augmenting path by the determined amount. Return the maximum flow.

Time Complexity: Time complexity of the above algorithm is O(max_flow * E). We run a loop while there is an augmenting path. In worst case, we may add 1 unit flow in every iteration. Therefore the time complexity becomes O(max_flow * E).

How to implement the above simple algorithm?  Let us first define the concept of Residual Graph which is needed for understanding the implementation. 

Residual Graph of a flow network is a graph which indicates additional possible flow. If there is a path from source to sink in residual graph, then it is possible to add flow. Every edge of a residual graph has a value called residual capacity which is equal to original capacity of the edge minus current flow. Residual capacity is basically the current capacity of the edge. 

Let us now talk about implementation details. Residual capacity is 0 if there is no edge between two vertices of residual graph. We can initialize the residual graph as original graph as there is no initial flow and initially residual capacity is equal to original capacity. To find an augmenting path, we can either do a BFS or DFS of the residual graph. We have used BFS in below implementation. Using BFS, we can find out if there is a path from source to sink. BFS also builds parent[] array. Using the parent[] array, we traverse through the found path and find possible flow through this path by finding minimum residual capacity along the path. We later add the found path flow to overall flow. 

The important thing is, we need to update residual capacities in the residual graph. We subtract path flow from all edges along the path and we add path flow along the reverse edges We need to add path flow along reverse edges because may later need to send flow in reverse direction (See following link for example). https://www.geeksforgeeks.org/max-flow-problem-introduction/

Below is the implementation of Ford-Fulkerson algorithm. To keep things simple, graph is represented as a 2D matrix. 

Time Complexity : O(|V| * E^2) ,where E is the number of edges and V is the number of vertices.

Space Complexity :O(V) , as we created queue.

The above implementation of Ford Fulkerson Algorithm is called Edmonds-Karp Algorithm . The idea of Edmonds-Karp is to use BFS in Ford Fulkerson implementation as BFS always picks a path with minimum number of edges. When BFS is used, the worst case time complexity can be reduced to O(VE 2 ). The above implementation uses adjacency matrix representation though where BFS takes O(V 2 ) time, the time complexity of the above implementation is O(EV 3 ) (Refer CLRS book for proof of time complexity)

This is an important problem as it arises in many practical situations. Examples include, maximizing the transportation with given traffic limits, maximizing packet flow in computer networks. Dinc’s Algorithm for Max-Flow.

Exercise:   Modify the above implementation so that it that runs in O(VE 2 ) time.

Similar Reads

Please login to comment..., improve your coding skills with practice.

What kind of Experience do you want to share?

Table of Contents

Minimum cost flow.

Author s : Siyong Huang, Benjamin Qi

Triangle Inequality, Johnson's Algorithm, and Min Cost Flow

Prerequisites

• Advanced - Maximum Flow

In this section I will briefly walk over my understanding of min cost flow. I would highly recommend reading through CP-Algorithm's Min Cost Flow to understand the solution idea first. Additionally, check the TopCoder tutorial for a more detailed explanation.

Triangle Inequality

In graph theory, the Triangle Inequality states that if there is an edge u → v u \rightarrow v u → v with weight w w w , and d k d_k d k ​ be the shortest path to node k k k (for some reasonable definition of shortest path), then d v − d u ≤ w d_v - d_u \leq w d v ​ − d u ​ ≤ w .

Johnson's Algorithm

The main idea of Johnson's Algorithm is that if all edge weights are positive, then running Dijkstra's from each node would result in a O ( V E log ⁡ E ) \mathcal{O}(VE \log E) O ( V E lo g E ) algorithm. If there are any negative edges, Johnson's Algorithm defines a potential function π \pi π , such that for every edge u , v , w u,v,w u , v , w , the following holds: w > = π ( u ) − π ( v ) w>=\pi(u)-\pi(v) w >= π ( u ) − π ( v ) . Then, each edge weight can be transformed into w → w + π ( v ) − π ( u ) w \rightarrow w + \pi(v)-\pi(u) w → w + π ( v ) − π ( u ) , resulting in positive weight. This condition coincides with the Triangle Inequality , so we can arbitrarily pick a node and run a O ( V E ) \mathcal{O}(VE) O ( V E ) shortest path algorithm to determine this function.

The general idea of Min Cost Flow is to repeatedly push flow along the shortest path. Since flow graphs have negative edges, each step naively would take O ( V E ) \mathcal{O}(VE) O ( V E ) time. To speed it up, we can use the same potential function from Johnson's Algorithm to employ Dijkstra for this process. In this case we must use distance from S S S , the source node, as the π \pi π function. At each step, run Dijkstra's using the π \pi π function, update the π \pi π function to match the current distances, and then push flow along the shortest path, reversing edges as needed. Once flow is met or the sink is unreachable, terminate.

Important Clarification

Note that the π \pi π function stores values before the edge reverses happen. Luckily the triangle inequality 's equality case is along the shortest path, meaning that in a flow network it holds both forwards and backwards along edges in the shortest path. This means that although the π \pi π function does not store the shortest paths, it still satisfies the triangle inequality for all edges.

π ( u ) − π ( v ) = w    ⟹    π ( v ) − π ( u ) = − w \pi(u)-\pi(v)=w \implies \pi(v)-\pi(u)=-w π ( u ) − π ( v ) = w ⟹ π ( v ) − π ( u ) = − w

Implementation

With all this being said, here is my implementation.

Also check out Benq's Implementation and KACTL's Implementation (which are a lot better than mine).

Applications

Assignment problem.

Focus Problem – try your best to solve this problem before continuing!

The assignment problem is best understood as a min cost max flow problem. In our formulation, we will assign W W W workers to J J J jobs, J ≥ W J \ge W J ≥ W , and the cost of assigning the i i i th job to the j j j th worker is C i , j C_{i,j} C i , j ​ .

We will create a flow network with a source node S S S , job nodes J i J_i J i ​ , worker nodes W j W_j W j ​ , and a sink node E E E .

We will have the following edges:

• ( S , J i ) (S, J_i) ( S , J i ​ ) with ( c a p a c i t y , c o s t ) = ( 1 , 0 ) (capacity, cost) = (1, 0) ( c a p a c i t y , cos t ) = ( 1 , 0 )
• ( J i , W j ) (J_i, W_j) ( J i ​ , W j ​ ) with ( 1 , C i , j ) (1, C_{i,j}) ( 1 , C i , j ​ )
• ( W j , E ) (W_j, E) ( W j ​ , E ) with ( 1 , 0 ) (1, 0) ( 1 , 0 )

The answer will be the minimum cost of the max flow of the graph. An example:

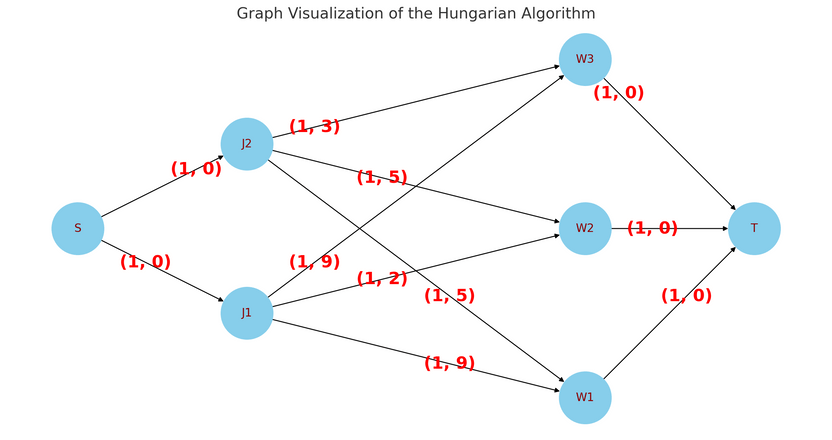
To solve this, we will use the min cost max flow algorithm detailed above. In every iteration of the algorithm, we will assign a job to a worker. In each iteration, we will first assign the job to an auxiliary worker, then we will try to find an augmenting path with minimum cost. To optimize this, we will only run Dijkstra on the worker nodes. For details, refer to the code.

Since there are J J J iterations (for each job) and each iteration takes O ( W 2 ) O(W^2) O ( W 2 ) time, the overall time complexity is O ( J W 2 ) O(J W^2) O ( J W 2 ) .

From Wikipedia (which is then copied from e-maxx):

Module Progress : Not Started

Join the usaco forum.

Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!

The assignment problem revisited

• Original Paper
• Published: 16 August 2021
• Volume 16 , pages 1531–1548, ( 2022 )

Cite this article

• Carlos A. Alfaro   ORCID: orcid.org/0000-0001-9783-8587 1 ,
• Sergio L. Perez 2 ,
• Carlos E. Valencia 3 &
• Marcos C. Vargas 1  

1109 Accesses

4 Citations

4 Altmetric

Explore all metrics

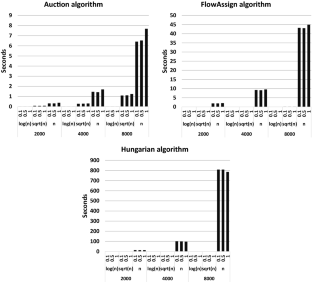
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for the assignment problem: the \(\epsilon \) - scaling auction algorithm , the Hungarian algorithm and the FlowAssign algorithm . The experiment shows that the auction algorithm still performs and scales better in practice than the other algorithms which are harder to implement and have better theoretical time complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Some results on an assignment problem variant

Integer Programming

A Full Description of Polytopes Related to the Index of the Lowest Nonzero Row of an Assignment Matrix

Bertsekas, D.P.: The auction algorithm: a distributed relaxation method for the assignment problem. Annal Op. Res. 14 , 105–123 (1988)

Article   MathSciNet   Google Scholar  

Bertsekas, D.P., Castañon, D.A.: Parallel synchronous and asynchronous implementations of the auction algorithm. Parallel Comput. 17 , 707–732 (1991)

Article   Google Scholar  

Bertsekas, D.P.: Linear network optimization: algorithms and codes. MIT Press, Cambridge, MA (1991)

MATH   Google Scholar  

Bertsekas, D.P.: The auction algorithm for shortest paths. SIAM J. Optim. 1 , 425–477 (1991)

Bertsekas, D.P.: Auction algorithms for network flow problems: a tutorial introduction. Comput. Optim. Appl. 1 , 7–66 (1992)

Bertsekas, D.P., Castañon, D.A., Tsaknakis, H.: Reverse auction and the solution of inequality constrained assignment problems. SIAM J. Optim. 3 , 268–299 (1993)

Bertsekas, D.P., Eckstein, J.: Dual coordinate step methods for linear network flow problems. Math. Progr., Ser. B 42 , 203–243 (1988)

Bertsimas, D., Tsitsiklis, J.N.: Introduction to linear optimization. Athena Scientific, Belmont, MA (1997)

Google Scholar  

Burkard, R., Dell’Amico, M., Martello, S.: Assignment Problems. Revised reprint. SIAM, Philadelphia, PA (2011)

Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18 (5), 1013–1036 (1989)

Goldberg, A.V., Tarjan, R.E.: A new approach to the maximum flow problem. J. Assoc. Comput. Mach. 35 , 921–940 (1988)

Goldberg, A.V., Tarjan, R.E.: Finding minimum-cost circulations by successive approximation. Math. Op. Res. 15 , 430–466 (1990)

Goldberg, A.V., Kennedy, R.: An efficient cost scaling algorithm for the assignment problem. Math. Programm. 71 , 153–177 (1995)

MathSciNet   MATH   Google Scholar  

Goldberg, A.V., Kennedy, R.: Global price updates help. SIAM J. Discr. Math. 10 (4), 551–572 (1997)

Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 83–97 (1955)

Kuhn, H.W.: Variants of the Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 253–258 (1956)

Lawler, E.L.: Combinatorial optimization: networks and matroids, Holt. Rinehart & Winston, New York (1976)

Orlin, J.B., Ahuja, R.K.: New scaling algorithms for the assignment ad minimum mean cycle problems. Math. Programm. 54 , 41–56 (1992)

Ramshaw, L., Tarjan, R.E., Weight-Scaling Algorithm, A., for Min-Cost Imperfect Matchings in Bipartite Graphs, : IEEE 53rd Annual Symposium on Foundations of Computer Science. New Brunswick, NJ 2012 , 581–590 (2012)

Zaki, H.: A comparison of two algorithms for the assignment problem. Comput. Optim. Appl. 4 , 23–45 (1995)

Download references

Acknowledgements

This research was partially supported by SNI and CONACyT.

Author information

Authors and affiliations.

Banco de México, Mexico City, Mexico

Carlos A. Alfaro & Marcos C. Vargas

Mountain View, CA, 94043, USA

Sergio L. Perez

Departamento de Matemáticas, CINVESTAV del IPN, Apartado postal 14-740, 07000, Mexico City, Mexico

Carlos E. Valencia

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Carlos A. Alfaro .

Ethics declarations

Conflict of interest.

There is no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were partially supported by SNI and CONACyT.

Rights and permissions

Reprints and permissions

About this article

Alfaro, C.A., Perez, S.L., Valencia, C.E. et al. The assignment problem revisited. Optim Lett 16 , 1531–1548 (2022). https://doi.org/10.1007/s11590-021-01791-4

Download citation

Received : 26 March 2020

Accepted : 03 August 2021

Published : 16 August 2021

Issue Date : June 2022

DOI : https://doi.org/10.1007/s11590-021-01791-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Assignment problem
• Bertsekas auction algorithm
• Combinatorial optimization and matching
• Find a journal
• Publish with us
• Track your research

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Assignment as a Minimum Cost Flow Problem

You can use the min cost flow solver to solve special cases of the assignment problem .

In fact, min cost flow can often return a solution faster than either the MIP or CP-SAT solver. However, MIP and CP-SAT can solve a larger class of problems than min cost flow, so in most cases MIP or CP-SAT are the best choices.

The following sections present Python programs that solve the following assignment problems using the min cost flow solver:

• A minimal linear assignment example .
• An assignment problem with teams of workers .

Linear assignment example

This section show how to solve the example, described in the section Linear Assignment Solver , as a min cost flow problem.

Import the libraries

The following code imports the required library.

Declare the solver

The following code creates the minimum cost flow solver.

Create the data

The flow diagram for the problem consists of the bipartite graph for the cost matrix (see the assignment overview for a slightly different example), with a source and sink added.

The data contains the following four arrays, corresponding to the start nodes, end nodes, capacities, and costs for the problem. The length of each array is the number of arcs in the graph.

To make clear how the data is set up, each array is divided into three sub-arrays:

• The first array corresponds to arcs leading out of the source.
• The second array corresponds to the arcs between workers and tasks. For the costs , this is just the cost matrix (used by the linear assignment solver), flattened into a vector.
• The third array corresponds to the arcs leading into the sink.

The data also includes the vector supplies , which gives the supply at each node.

How a min cost flow problem represents an assignment problem

How does the min cost flow problem above represent an assignment problem? First, since the capacity of every arc is 1, the supply of 4 at the source forces each of the four arcs leading into the workers to have a flow of 1.

Next, the flow-in-equals-flow-out condition forces the flow out of each worker to be 1. If possible, the solver would direct that flow across the minimum cost arc leading out of each worker. However, the solver cannot direct the flows from two different workers to a single task. If it did, there would be a combined flow of 2 at that task, which couldn't be sent across the single arc with capacity 1 from the task to the sink. This means that the solver can only assign a task to a single worker, as required by the assignment problem.

Finally, the flow-in-equals-flow-out condition forces each task to have an outflow of 1, so each task is performed by some worker.

Create the graph and constraints

The following code creates the graph and constraints.

Invoke the solver

The following code invokes the solver and displays the solution.

The solution consists of the arcs between workers and tasks that are assigned a flow of 1 by the solver. (Arcs connected to the source or sink are not part of the solution.)

The program checks each arc to see if it has flow 1, and if so, prints the Tail (start node) and the Head (end node) of the arc, which correspond to a worker and task in the assignment.

Output of the program

Here is the output of the program.

The result is the same as that for the linear assignment solver (except for the different numbering of workers and costs). The linear assignment solver is slightly faster than min cost flow — 0.000147 seconds versus 0.000458 seconds.

The entire program

The entire program is shown below.

Assignment with teams of workers

This section presents a more general assignment problem. In this problem, six workers are divided into two teams. The problem is to assign four tasks to the workers so that the workload is equally balanced between the teams — that is, so each team performs two of the tasks.

For a MIP solver solution to this problem see Assignment with Teams of Workers .

The following sections describe a program that solves the problem using the min cost flow solver.

The following code creates the data for the program.

The workers correspond to nodes 1 - 6. Team A consists of workers 1, 3, and 5, and team B consists of workers 2, 4, and 6. The tasks are numbered 7 - 10.

There are two new nodes, 11 and 12, between the source and workers. Node 11 is connected to the nodes for team A, and Node 12 is connected to the nodes for team B, with arcs of capacity 1. The graph below shows just the nodes and arcs from the source to the workers.

The key to balancing the workload is that the source 0 is connected to nodes 11 and 12 by arcs of capacity 2. This means that nodes 11 and 12 (and therefore teams A and B) can have a maximum flow of 2. As a result, each team can perform at most two of the tasks.

Create the constraints

The following shows the output of the program.

Team A is assigned tasks 9 and 10, while team B is assigned tasks 7 and 8.

Note that the min cost flow solver is faster for this problem than the MIP solver , which takes around 0.006 seconds.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2024-08-28 UTC.

Network flow problem

Author: Aaron Wheeler, Chang Wei, Cagla Deniz Bahadir, Ruobing Shui, Ziqiu Zhang (ChemE 6800 Fall 2020)

• 1 Introduction
• 2.1.1 The Assignment Problem
• 2.1.2 The Transportation Problem
• 2.1.3 The Shortest-Path Problem
• 2.1.4 Maximal Flow Problem
• 2.2.1 Ford–Fulkerson Algorithm
• 3.1 Formulation of the Problem
• 3.2 Solution of the Problem
• 4.1 The Minimum Cost Flow Problem
• 4.2 The Assignment Problem
• 4.3 The Shortest Path Problem
• 5 Conclusion
• 6 References

Introduction

Network flow problems arise in several key instances and applications within society and have become fundamental problems within computer science, operations research, applied mathematics, and engineering. Developments in the approach to tackle these problems resulted in algorithms that became the chief instruments for solving problems related to large-scale systems and industrial logistics. Spurred by early developments in linear programming, the methods for addressing these extensive problems date back several decades and they evolved over time as the use of digital computing became increasingly prevalent in industrial processes. Historically, the first instance of an algorithmic development for the network flow problem came in 1956, with the network simplex method formulated by George Dantzig. [1] A variation of the simplex algorithm that revolutionized linear programming, this method leveraged the combinatorial structure inherent to these types of problems and demonstrated incredibly high accuracy. [2] This method and its variations would go on to define the embodiment of the algorithms and models for the various and distinct network flow problems discussed here.

Theory, Methodology, and Algorithms

Additional constraints of the network flow optimization model place limits on the solution and vary significantly based on the specific type of problem being solved. Historically, the classic network flow problems are considered to be the maximum flow problem and the minimum-cost circulation problem, the assignment problem, bipartite matching problem, transportation problem, and the transshipment problem. [2] The approach to these problems become quite specific based upon the problem’s objective function but can be generalized by the following iterative approach: 1. determining the initial basic feasible solution; 2. checking the optimality conditions (i.e. whether the problem is infeasible, unbounded over the feasible region, optimal solution has been found, etc.); and 3. constructing an improved basic feasible solution if the optimal solution has not been determined. [3]

General Applications

The assignment problem.

Various real-life instances of assignment problems exist for optimization, such as assigning a group of people to different tasks, events to halls with different capacities, rewards to a team of contributors, and vacation days to workers. All together, the assignment problem is a bipartite matching problem in the kernel. [3] In a classical setting, two types of objects of equal amount are  bijective (i.e. they have one-to-one matching), and this tight constraint ensures a perfect matching. The objective is to minimize the cost or maximize the profit of matching, since different items of two types have distinct affinity.

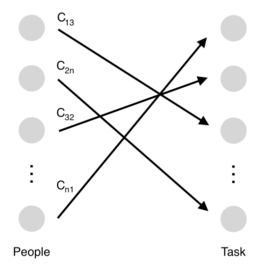
Figure 2 can be viewed as a network. The nodes represent people and tasks, and the edges represent potential assignments between a person and a task. Each task can be completed by any person. However, the person that actually ends up being assigned to the task will be the lone individual who is best suited to complete. In the end, the edges with positive flow values will be the only ones represented in the finalized assignment. [5]

The concise-form formulation of the problem is as follows [3] :

Subject to:

The first constraint captures the requirement of assigning each person  to a single task. The second constraint indicates that each task must be done by exactly one person. The objective function sums up the overall benefits of all assignments.

To see the analogy between the assignment problem and the network flow, we can describe each person supplying a flow of 1 unit and each task demanding a flow of 1 unit, with the benefits over all “channels” being maximized. [3]

A potential issue lies in the branching of the network, specifically an instance where a person splits its one unit of flow into multiple tasks and the objective remains maximized. This shortcoming is allowed by the laws that govern the network flow model, but are unfeasible in real-life instances. Fortunately, since the network simplex method only involves addition and subtraction of a single edge while transferring the basis, which is served by the spanning tree of the flow graph, if the supply (the number of people here) and the demand (the number of tasks here) in the constraints are integers, the solved variables will be automatically integers even if it is not explicitly stated in the problem. This is called the integrality of the network problem, and it certainly applies to the assignment problem. [6]

The Transportation Problem

People first came up with the transportation problem when distributing troops during World War II. [7] Now, it has become a useful model for solving logistics problems, and the objective is usually to minimize the cost of transportation.

Consider the following scenario:

Several quantities should be defined to help formulate the frame of the solution:

Here, the amount of material being delivered and being consumed is bound to the supply and demand constraints:

The objective is to find the minimum cost of transportation, so the cost of each transportation line should be added up, and the total cost should be minimized.

Using the definitions above, the problem can be formulated as such:

The problem and the formulation is adapted from Chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti. [3]

The Shortest-Path Problem

The shortest-path problem can be defined as finding the path that yields the shortest total distance between the origin and the destination. Each possible stop is a node and the paths between these nodes are edges incident to these nodes, where the path distance becomes the weight of the edges. In addition to being the most common and straightforward application for finding the shortest path, this model is also used in various applications depending on the definition of nodes and edges. [3] For example, when each node represents a different object and the edge specifies the cost of replacement, the equipment replacement problem is derived. Moreover, when each node represents a different project and the edge specifies the relative priority, the model becomes a project scheduling problem.

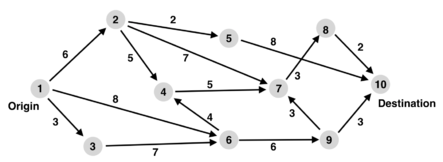
A graph of the general shortest-path problem is depicted as Figure 4:

The first term of the constraint is the total outflow of the node i, and the second term is the total inflow. So, the formulation above could be seen as one unit of flow being supplied by the origin, one unit of flow being demanded by the destination, and no net inflow or outflow at any intermediate nodes. These constraints mandate a flow of one unit, amounting to the active path, from the origin to the destination. Under this constraint, the objective function minimizes the overall path distance from the origin to the destination.

Similarly, the integrality of the network problem applies here, precluding the unreasonable fractioning. With supply and demand both being integer (one here), the edges can only have integer amount of flow in the result solved by simplex method. [6]

In addition, the point-to-point model above can be further extended to other problems. A number of real life scenarios require visiting multiple places from a single starting point. This “Tree Problem” can be modeled by making small adjustments to the original model. In this case, the source node should supply more units of flow and there will be multiple sink nodes demanding one unit of flow. Overall, the objective and the constraint formulation are similar. [4]

Maximal Flow Problem

This problem describes a situation where the material from a source node is sent to a sink node. The source and sink node are connected through multiple intermediate nodes, and the common optimization goal is to maximize the material sent from the source node to the sink node. [3]

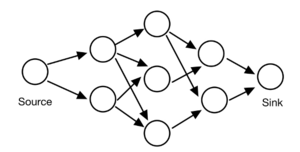
The given structure is a piping system. The water flows into the system from the source node, passing through the intermediate nodes, and flows out from the sink node. There is no limitation on the amount of water that can be used as the input for the source node. Therefore, the sink node can accept an unlimited amount of water coming into it. The arrows denote the valid channel that water can flow through, and each channel has a known flow capacity. What is the maximum flow that the system can take?

For the source and sink node, they have net flow that is non-zero:

Flow capacity definition is applied to all nodes (including intermediate nodes, the sink, and the source):

The main constraints for this problem are the transport capacity between each node and the material conservation:

Overall, the net flow out of the source node has to be the same as the net flow into the sink node. This net flow is the amount that should be maximized.

Using the definitions above:

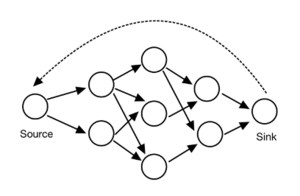
This expression can be further simplified by introducing an imaginary flow from the sink to the source.

By introducing this imaginary flow, the piping system is now closed. The mass conservation constraint now also holds for the source and sink node, so they can be treated as the intermediate nodes. The problem can be rewritten as the following: 

The problem and the formulation are derived from an example in Chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti. [3]

Ford–Fulkerson Algorithm

A broad range of network flow problems could be reduced to the max-flow problem. The most common way to approach the max-flow problem in polynomial time is the Ford-Fulkerson Algorithm (FFA). FFA is essentially a greedy algorithm and it iteratively finds the augmenting s-t path to increase the value of flow. The pathfinding terminates until there is no s-t path present. Ultimately, the max-flow pattern in the network graph will be returned. [8]

Numerical Example and Solution

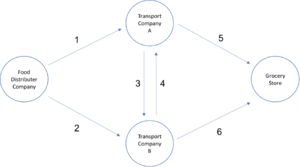
A Food Distributor Company is farming and collecting vegetables from farmers to later distribute to the grocery stores. The distributor has specific agreements with different third-party companies to mediate the delivery to the grocery stores. In a particular month, the company has 600 ton vegetables to deliver to the grocery store. They have agreements with two third-party transport companies A and B, which have different tariffs for delivering goods between themselves, the distributor, and the grocery store. They also have limits on transport capacity for each path. These delivery points are numbered as shown below, with path 1 being the transport from the Food Distributor Company to the transport company A. The limits and tariffs for each path can be found in the Table 2 below, and the possible transportation connections between the distributor company, the third-party transporters, and the grocery store are shown in the figure below. The distributor companies cannot hold any amount of food, and any incoming food should be delivered to an end point. The distributor company wants to minimize the overall transport cost of shipping 600 tons of vegetables to the grocery store by choosing the optimal path provided by the transport companies. How should the distributor company map out their path and the amount of vegetables carried on each path to minimize cost overall?

This question is adapted from one of the exercise questions in chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti [3] .

Formulation of the Problem

The second step is to write down the constraints. The first constraint ensures that the net amount present in the Transport Company A, which is the deliveries received from path 1 and path 2 minus the transport to Transport Company B should be delivered to the grocery store with path 5. The second constraint ensures this for the Transport Company B. The third and fourth constraints are ensuring that the total amount of vegetables shipping from the Food Distributor Company and the total amount of vegetables delivered to the grocery store are both 600 tons. The constraints 5 to 10 depict the upper limits of the amount of vegetables that can be carried on paths 1 to 6. The final constraint depicts that all variables are non-negative.

Solution of the Problem

This problem can be solved using Simplex Algorithm [11] or with the CPLEX Linear Programming solver in GAMS optimization platform. The steps of the solution using the GAMS platform is as follows:

variables x1,x2,x3,x4,x5,x6,z;

obj.. z=e= 10*x1+12.5*x2+5*x3+7.5*x4+10*x5+20*x6;

Overall, there are 10 constraints in this problem. The constraints 1, and 2 are equations for the paths 5 and 6. The amount carried in path 5 can be found by summing the amount of vegetables incoming to Transport Company A from path 1 and path 4, minus the amount of vegetables leaving Transport Company A with path 3. This can be attributed to the restriction that barrs the companies from keeping any vegetables and requires them to eventually deliver all the incoming produce. The equality 1 ensures that this constraint holds for path 5 and equation 2 ensures it for path 6. A sample of these constraints is written below for path 5:

c1.. x5 =e=x1-x3+x4;

Constraint 3 ensures that the sum of vegetables carried in path 1 and path 2 add to the total of 600 tons of vegetables that leave the Food Distributor Company. Likewise, the constraint 4 ensures that the sum amount of food transported in paths 5 and 6 adds up to 600 tons of vegetables that have to be delivered to the grocery store. A sample of these constraints is written below for the total delivery to the grocery store:

c3.. x5+x6=e=600;

Constraints 5 to 10 should ensure that the amount of food transported in each path should not exceed the maximum capacity depicted in the table. A sample of these constraints is written below for the capacity of path 1:

c5.. x1=l=250;

After listing the variables, objective function and the constraints, the final step is to call the CPLEX solver and set the type of the optimization problem as lp (linear programming). In this case the problem will be solved with a Linear Programming algorithm to minimize the objective (cost) function.

The GAMS code yields the results below:

x1 = 250, x2 = 350, x3 = 0, x4 = 50, x5 = 300, x6 = 300, z =16250.

Real Life Applications

Network problems have many applications in all kinds of areas such as transportation, city design, resource management and financial planning. [6]

There are several special cases of network problems, such as the shortest path problem, minimum cost flow problem, assignment problem and transportation problem. [6] Three application cases will be introduced here.

The Minimum Cost Flow Problem

Minimum cost flow problems are pervasive in real life, such as deciding how to allocate temporal quay crane in container terminals, and how to make optimal train schedules on the same railroad line. [12]

R. Dewil and his group use MCNFP to assist traffic enforcement. [13] Police patrol “hot spots”, which are areas where crashes occur frequently on highways. R. Dewil studies a method intended to estimate the optimal route of hot spots. He describes the time it takes to move the detector to a certain position as the cost, and the number of patrol cars from one node to next as the flow, in order to minimize the total cost. [13]

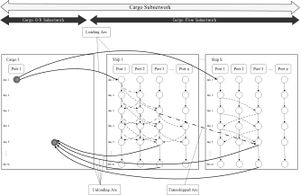
Dung-Ying Lin studies an assignment problem in which he aims to assign freights to ships and arrange transportation paths along the Northern Sea Route in a manner which yields maximum profit. [14] Within this network  composed of a ship subnetwork and a cargo subnetwork( shown as Figure 12 and Figure 13), each node corresponds to a port at a specific time and each arc represents the movement of a ship or a cargo. Other types of assignment problems are faculty scheduling, freight assignment, and so on.

The Shortest Path Problem

Shortest path problems are also present in many fields, such as transportation, 5G wireless communication, and implantation of the global dynamic routing scheme. [15][16][17]

Qiang Tu and his group studies the constrained reliable shortest path (CRSP) problem for electric vehicles in the urban transportation network. [15] He describes the reliable travel time of path as the objective item, which is made up of planning travel time of path and the reliability item. The group studies the Chicago sketch network consisting of 933 nodes and 2950 links and the Sioux Falls network consisting of 24 nodes and 76 links. The results show that the travelers’ risk attitudes and properties of electric vehicles in the transportation network can have a great influence on the path choice. [15] The study can contribute to the invention of the city navigation system.

Since its inception, the network flow problem has provided humanity with a straightforward and scalable approach for several large-scale challenges and problems. The Simplex algorithm and other computational optimization platforms have made addressing these problems routine, and have greatly expedited efforts for groups concerned with supply-chain and other distribution processes. The formulation of this problem has had several derivations from its original format, but its overall methodology and approach have remained prevalent in several of society’s industrial and commercial processes, even over half a century later. Classical models such as the assignment, transportation, maximal flow, and shortest path problem configurations have found their way into diverse settings, ranging from streamlining oil distribution networks along the gulf coast to arranging optimal scheduling assignments for college students amidst a global pandemic. All in all, the network flow problem and its monumental impact, have made it a fundamental tool for any group that deals with combinatorial data sets. And with the surge in adoption of data-driven models and applications within virtually all industries, the use of the network flow problem approach will only continue to drive innovation and meet consumer demands for the foreseeable future.

1. Karp, R. M. (2008). George Dantzig’s impact on the theory of computation . Discrete Optimization, 5(2), 174-185.

2. Goldberg, A. V. Tardos, Eva, Tarjan, Robert E. (1989). Network Flow Algorithms, Algorithms and Combinatorics . 9. 101-164.

3. Bradley, S. P. Hax, A. C., & Magnanti, T. L. (1977). Network Models. Applied mathematical programming (p. 259). Reading, MA: Addison-Wesley.

4. Chinneck, J. W. (2006). Practical optimization: a gentle introduction. Systems and Computer Engineering . Carleton University, Ottawa. 11.

5. Roy, B. V. Mason, K.(2005). Formulation and Analysis of Linear Programs, Chapter 5 Network Flows .

6. Vanderbei, R. J. (2020). Linear programming: foundations and extensions (Vol. 285) . Springer Nature.

7. Sobel, J. (2014). Linear Programming Notes VIII: The Transportation Problem .

8. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 26.2: The Ford–Fulkerson method". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill.

9. Jon Kleinberg; Éva Tardos (2006). "Chapter 7: Network Flow". Algorithm Design. Pearson Education.

10. Ford–Fulkerson algorithm . Retrieved December 05, 2020.

11. Hu, G. (2020, November 19). Simplex algorithm . Retrieved November 22, 2020.

12. Altınel, İ. K., Aras, N., Şuvak, Z., & Taşkın, Z. C. (2019). Minimum cost noncrossing flow problem on layered networks . Discrete Applied Mathematics, 261, 2-21.

13. Dewil, R., Vansteenwegen, P., Cattrysse, D., & Van Oudheusden, D. (2015). A minimum cost network flow model for the maximum covering and patrol routing problem . European Journal of Operational Research, 247(1), 27-36.

14. Lin, D. Y., & Chang, Y. T. (2018). Ship routing and freight assignment problem for liner shipping: Application to the Northern Sea Route planning problem . Transportation Research Part E: Logistics and Transportation Review, 110, 47-70.

15. Tu, Q., Cheng, L., Yuan, T., Cheng, Y., & Li, M. (2020). The Constrained Reliable Shortest Path Problem for Electric Vehicles in the Urban Transportation Network . Journal of Cleaner Production, 121130.

16. Guo, Y., Li, S., Jiang, W., Zhang, B., & Ma, Y. (2017). Learning automata-based algorithms for solving the stochastic shortest path routing problems in 5G wireless communication . Physical Communication, 25, 376-385.

17. Haddou, N. B., Ez-Zahraouy, H., & Rachadi, A. (2016). Implantation of the global dynamic routing scheme in scale-free networks under the shortest path strategy . Physics Letters A, 380(33), 2513-2517.

Navigation menu

• Implementation
• Practice Problems
• Assignment problem

Minimum-cost flow - Successive shortest path algorithm ¶

Given a network $G$ consisting of $n$ vertices and $m$ edges. For each edge (generally speaking, oriented edges, but see below), the capacity (a non-negative integer) and the cost per unit of flow along this edge (some integer) are given. Also the source $s$ and the sink $t$ are marked.

For a given value $K$ , we have to find a flow of this quantity, and among all flows of this quantity we have to choose the flow with the lowest cost. This task is called minimum-cost flow problem .

Sometimes the task is given a little differently: you want to find the maximum flow, and among all maximal flows we want to find the one with the least cost. This is called the minimum-cost maximum-flow problem .

Both these problems can be solved effectively with the algorithm of successive shortest paths.

Algorithm ¶

This algorithm is very similar to the Edmonds-Karp for computing the maximum flow.

Simplest case ¶

First we only consider the simplest case, where the graph is oriented, and there is at most one edge between any pair of vertices (e.g. if $(i, j)$ is an edge in the graph, then $(j, i)$ cannot be part in it as well).

Let $U_{i j}$ be the capacity of an edge $(i, j)$ if this edge exists. And let $C_{i j}$ be the cost per unit of flow along this edge $(i, j)$ . And finally let $F_{i, j}$ be the flow along the edge $(i, j)$ . Initially all flow values are zero.

We modify the network as follows: for each edge $(i, j)$ we add the reverse edge $(j, i)$ to the network with the capacity $U_{j i} = 0$ and the cost $C_{j i} = -C_{i j}$ . Since, according to our restrictions, the edge $(j, i)$ was not in the network before, we still have a network that is not a multigraph (graph with multiple edges). In addition we will always keep the condition $F_{j i} = -F_{i j}$ true during the steps of the algorithm.

We define the residual network for some fixed flow $F$ as follow (just like in the Ford-Fulkerson algorithm): the residual network contains only unsaturated edges (i.e. edges in which $F_{i j} < U_{i j}$ ), and the residual capacity of each such edge is $R_{i j} = U_{i j} - F_{i j}$ .

Now we can talk about the algorithms to compute the minimum-cost flow. At each iteration of the algorithm we find the shortest path in the residual graph from $s$ to $t$ . In contrast to Edmonds-Karp, we look for the shortest path in terms of the cost of the path instead of the number of edges. If there doesn't exists a path anymore, then the algorithm terminates, and the stream $F$ is the desired one. If a path was found, we increase the flow along it as much as possible (i.e. we find the minimal residual capacity $R$ of the path, and increase the flow by it, and reduce the back edges by the same amount). If at some point the flow reaches the value $K$ , then we stop the algorithm (note that in the last iteration of the algorithm it is necessary to increase the flow by only such an amount so that the final flow value doesn't surpass $K$ ).

It is not difficult to see, that if we set $K$ to infinity, then the algorithm will find the minimum-cost maximum-flow. So both variations of the problem can be solved by the same algorithm.

Undirected graphs / multigraphs ¶

The case of an undirected graph or a multigraph doesn't differ conceptually from the algorithm above. The algorithm will also work on these graphs. However it becomes a little more difficult to implement it.

An undirected edge $(i, j)$ is actually the same as two oriented edges $(i, j)$ and $(j, i)$ with the same capacity and values. Since the above-described minimum-cost flow algorithm generates a back edge for each directed edge, so it splits the undirected edge into $4$ directed edges, and we actually get a multigraph .

How do we deal with multiple edges ? First the flow for each of the multiple edges must be kept separately. Secondly, when searching for the shortest path, it is necessary to take into account that it is important which of the multiple edges is used in the path. Thus instead of the usual ancestor array we additionally must store the edge number from which we came from along with the ancestor. Thirdly, as the flow increases along a certain edge, it is necessary to reduce the flow along the back edge. Since we have multiple edges, we have to store the edge number for the reversed edge for each edge.

There are no other obstructions with undirected graphs or multigraphs.

Complexity ¶

The algorithm here is generally exponential in the size of the input. To be more specific, in the worst case it may push only as much as $1$ unit of flow on each iteration, taking $O(F)$ iterations to find a minimum-cost flow of size $F$ , making a total runtime to be $O(F \cdot T)$ , where $T$ is the time required to find the shortest path from source to sink.

If Bellman-Ford algorithm is used for this, it makes the running time $O(F mn)$ . It is also possible to modify Dijkstra's algorithm , so that it needs $O(nm)$ pre-processing as an initial step and then works in $O(m \log n)$ per iteration, making the overall running time to be $O(mn + F m \log n)$ . Here is a generator of a graph, on which such algorithm would require $O(2^{n/2} n^2 \log n)$ time.

The modified Dijkstra's algorithm uses so-called potentials from Johnson's algorithm . It is possible to combine the ideas of this algorithm and Dinic's algorithm to reduce the number of iterations from $F$ to $\min(F, nC)$ , where $C$ is the maximum cost found among edges. You may read further about potentials and their combination with Dinic algorithm here .

Implementation ¶

Here is an implementation using the SPFA algorithm for the simplest case.

Practice Problems ¶

• CSES - Task Assignment
• CSES - Grid Puzzle II
• AtCoder - Dream Team
• jakobkogler (85.12%)
• adamant-pwn (5.96%)
• prprprpony (4.76%)
• fffelix-huang (2.98%)
• maiquang04 (0.6%)
• hieplpvip (0.6%)