two sample mean hypothesis test calculator

Two Sample T-Test Calculator (Pooled-Variance)

Enter sample data, information, assumptions, required sample data.

Difference in Means Hypothesis Test Calculator

Use the calculator below to analyze the results of a difference in sample means hypothesis test. Enter your sample means, sample standard deviations, sample sizes, hypothesized difference in means, test type, and significance level to calculate your results.

You will find a description of how to conduct a two sample t-test below the calculator.

Define the Two Sample t-test

The difference between the sample means under the null distribution, conducting a hypothesis test for the difference in means.

When two populations are related, you can compare them by analyzing the difference between their means.

A hypothesis test for the difference in samples means can help you make inferences about the relationships between two population means.

Testing for a Difference in Means

For the results of a hypothesis test to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Independence of Samples - Your samples should be collected independently of one another.
• Simple Random Sampling - You should collect your samples with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normality of Sample Distributions - The sampling distributions for both samples should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct an hypothesis test of the difference in means.

The null hypothesis is a skeptical claim that you would like to test.

The alternative hypothesis represents the alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

D is the hypothesized difference between the populations' means that you would like to test.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ 1 - μ 2 ≠ D requires a two tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null distribution. For example, in a one-tail test evaluating if the actual difference in means, D, is above the null distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ 1 - μ 2 > D and μ 1 - μ 2 < D alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal distribution with the following parameters:

• The Difference in the Population Means, D - The true difference in the population means is unknown, but we use the hypothesized difference in the means, D, from the null hypothesis in the calculations.
• The Standard Error, SE - The standard error of the difference in the sample means can be computed as follows:      SE = (s 1 2 /n 1 + s 2 2 /n 2 ) (1/2) with s 1 being the standard deviation of sample one, n 1 being the sample size of sample one, s 2 being the standard deviation of sample one, and n 2 being the sample size of sample two. The standard error defines how differences in sample means are expected to vary around the null difference in means sampling distribution given the sample sizes and under the assumption that the null hypothesis is true.
• The Degrees of Freedom, DF - The degrees of freedom calculation can be estimated as the smaller of n 1 - 1 or n 2 - 1. For more accurate results, use the following formula for the degrees of freedom (DF):      DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / ((s 1 2 /n 1 ) 2 / (n 1 - 1) + (s 2 2 /n 2 ) 2 / (n 2 - 1))

In a difference in means hypothesis test, we calculate the probability that we would observe the difference in sample means (x̄ 1 - x̄ 2 ), assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ 1 - x̄ 2 - D) / SE

The t-score is a test statistic that tells you how far our observation is from the null hypothesis's difference in means under the null distribution. Using any t-score table, you can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for the difference in means is sometimes known as a two sample mean t-test because of the use of a t-score in analyzing results.

The conclusion of a hypothesis test for the difference in means is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample difference in means is the true difference between the means. If you do not reject the null hypothesis, you cannot say that the hypothesized difference in means is true.

A hypothesis test is simply a way to look at evidence and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for the Difference in Two Means

Let’s say you are a manager at a company that designs batteries for smartphones. One of your engineers believes that she has developed a battery that will last more than two hours longer than your standard battery.

Before you can consider if you should replace your standard battery with the new one, you need to test the engineer’s claim. So, you decided to run a difference in means hypothesis test to see if her claim that the new battery will last two hours longer than the standard one is reasonable.

You direct your team to run a study. They will take a sample of 100 of the new batteries and compare their performance to 1,000 of the old standard batteries.

• Check the conditions - Your test consists of independent samples . Your team collects your samples using simple random sampling , and you have reason to believe that all your batteries' performances are always close to normally distributed . So, the conditions are met to conduct a two sample t-test.
• State Your Hypothesis - Your null hypothesis is that the charge of the new battery lasts at most two hours longer than your standard battery (i.e. μ 1 - μ 2 ≤ 2). Your alternative hypothesis is that the new battery lasts more than two hours longer than the standard battery (i.e. μ 1 - μ 2 > 2).
• Determine Your Analysis Plan - You believe that a 1% significance level is reasonable. As your test is a one-tail test, you will evaluate if the difference in mean charge between the samples would occur at the upper 1% of the null distribution.
• Analyze Your Sample - After collecting your samples (which you do after steps 1-3), you find the new battery sample had a mean charge of 10.4 hours, x̄ 1 , with a 0.8 hour standard deviation, s 1 . Your standard battery sample had a mean charge of 8.2 hours, x̄ 2 , with a standard deviation of 0.2 hours, s 2 . Using the calculator above, you find that a difference in sample means of 2.2 hours [2 = 10.4 – 8.2] would results in a t-score of 2.49 under the null distribution, which translates to a p-value of 0.72%.
• Interpret Your Results - Since your p-value of 0.72% is less than the significance level of 1%, you have sufficient evidence to reject the null hypothesis.

In this example, you found that you can reject your null hypothesis that the new battery design does not result in more than 2 hours of extra battery life. The test does not guarantee that your engineer’s new battery lasts two hours longer than your standard battery, but it does give you strong reason to believe her claim.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Statistics and probability
• T-test calculator

T-Test calculator

The Student's t-test is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t – test.

Get Widget Code

• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Twelve younger adults and twelve older adults conducted a life satisfaction test. The data are presented in the table below. Compute the appropriate t-test.

Are the means between two data sets are significantly different at level $\alpha < 0.05$.

Standard deviation calculator – Widget Code

Feel free to copy the widget code below and paste it into your website or blog. The widget will look like the example below.

Widget preview: Standard deviation calculator

Copy code to clipboard

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

•  All online calculators
•  Suggest a calculator
•  Translation

PLANETCALC Online calculators

•  English

Two sample t-Test

The calculator to perform t-Test for the Significance of the Difference between the Means of Two Independent Samples

The calculator below implements the most known statistical test, namely, the Independent Samples t-test or Two samples t-test. t-test, also known as Student's t-test, after William Sealy Gosset. "Student" was his pen name.

The test deals with the null hypothesis such that the means of two populations are equal. To put it in other words, the difference we find between the means of the two samples should not significantly differ from zero.

Again, the test works only if certain assumptions are met. These are:

• That the two samples are independently and randomly drawn from the source population(s).
• That the scale of measurement for both samples has the properties of an equal-interval scale.
• That the source population(s) can be reasonably supposed to have a normal distribution.
• And, for this particular implementation of the test, that the variance of each population is the same

The calculator displays a level of confidence for both directional and non-directional tests. Let's say you get the result of 96%. Essentially this means that you have 96% confidence that the obtained difference shows something more than simple luck. The chance that you can get the obtained difference and the means of the two samples are the same is only 4%. This is the level of significance you calculate. Now, depending on your chosen level of significance, you can reject or fail to reject your null hypothesis.

If you care to find more, you can read excellent explanations here , starting from Chapter 9.

Two samples t-Test

Similar calculators.

• • Student t-distribution
• • PlanetCalc statistics
• • P-value
• • Estimated Mean of a Population
• • Binomial distribution, probability density function, cumulative distribution function, mean and variance
• • Statistics section ( 37 calculators )

Share this page

• PRE-ALGEBRA
• MORE MATH FINANCE BUSINESS ENGINEERING FINANCE CHARTS MATH WORKSHEETS CURRENCY CONVERTER MULTIPLICATION TABLES DEPRECIATION SPORTS CALCULATORS HEALTH equations tricks history notes register login

• Engineering

t-Test Calculator

T-test - work with steps.

Input Data : Data set x = 3, 11, 17, 28, 34 Data set y = 5, 8, 13, 19, 28 Total number of elements = 5 Objective : Find the t-score by using mean and standard deviation. Solution : Mean 1 = (3 + 11 + 17 + 28 + 34)/5 = 93/5 Mean 1 = 18.6 Mean 2 = (5 + 8 + 13 + 19 + 28)/5 = 73/5 Mean 2 = 14.6 SD1 = √(1/5 - 1) x ((3 - 18.6) 2 + ( 11 - 18.6) 2 + ( 17 - 18.6) 2 + ( 28 - 18.6) 2 + ( 34 - 18.6) 2 ) = √(1/4) x ((-15.6) 2 + (-7.6) 2 + (-1.6) 2 + (9.4) 2 + (15.4) 2 ) = √(0.25) x ((243.36) + (57.76) + (2.56) + (88.36) + (237.16)) = √(0.25) x 629.2 = √157.3 SD1 = 12.5419 SD2 = √(1/5 - 1) x ((5 - 14.6) 2 + ( 8 - 14.6) 2 + ( 13 - 14.6) 2 + ( 19 - 14.6) 2 + ( 28 - 14.6) 2 ) = √(1/4) x ((-9.6) 2 + (-6.6) 2 + (-1.6) 2 + (4.4) 2 + (13.4) 2 ) = √(0.25) x ((92.16) + (43.56) + (2.56) + (19.36) + (179.56)) = √(0.25) x 337.2 = √84.3 SD2 = 9.1815 t-score = x 1 - x 2 √(SD1 2 /n1 + SD2 2 /n2) = 18.6 - 14.6 √((12.5419) 2 /5 + (9.1815) 2 /5) = 4 √((157.3)/5 + (84.3)/5) = 4 √(31.46 + 16.86) = 4 √(48.32) = 4 6.9513 t-score = 0.5754

t-test calculator is an online statistics tool to estimate the significance of observed differences between the means of two samples when there is a null hypothesis that is no significant difference between the means by using standard deviation. It is necessary to follow the next steps:

• Enter two samples (observed values) in the box. These values must be real numbers or variables and may be separated by commas. The values can be copied from a text document or a spreadsheet.
• Press the "GENERATE WORK" button to make the computation.
• t-Test calculator will give a test whether samples from two independent populations provide that the populations have different means.

What is t-Test?

A hypothesis test consists of two hypotheses, the null hypothesis and the alternative hypothesis or research hypothesis. The symbol $H_0$ represents the null hypothesis. The null hypothesis reflects that there will be no observed effect on the experiment. The null hypothesis consists of an equal sign. The alternative hypothesis reflects that there is an observed effect on the experiment. The symbol $H_a$ represents the alternative hypothesis. The first step in testing is to determine the null hypothesis and the alternative hypothesis. Regarding the testing hypothesis, there are some important terms. Rejection region is the set of values leads to rejection of the null hypothesis. Non-rejection region is the set of values that leads to nonrejection of the null hypothesis. Critical values are the value that separates the rejection and non-rejection regions. The t-Test is used in comparing the means of two populations. There are two approaches:

• When the samples from the two populations are independent;
• When the samples from the two populations are depended, i.e. when they are paired.
• If populations standard deviations are equal, $\sigma_1-\sigma_2$
• If populations standard deviations are different

How to Find t-Critical Value

To perform a hypothesis test to compare two population means, $\mu_1$ and $\mu_2$, we have some assumptions:

• Simple and independent random samples;
• Normal populations or large samples.

t-Test with Mean and Standard Deviation

A t-Test is one of the most frequently used tests in statistics. A t-Test is useful to conclude if the results are correct and applicable to the entire population. If we want to analyze simple experiments or when making simple comparisons between levels of independent variable we use the t-Test. It's used in comparison between two separate groups of individuals, for example: male vs female, experimental vs control group, etc. Practice Problem 1: There are two company A and B. We want to test average age of employees at these companies so we use a random sample of employee ages from each company.

• Hypergeometric distribution Calculator
• Error Function Calculator
• Beta Function Calculator
• Gamma Function Calculator
• Digamma Function Calculator
• F-Test Calculator
• Statistical Data Set Range Calculator
• Effect of Size Calculator
• Sampling Error Calculator
• Percent Error Calculator
• Percentile Calculator
• Signal to Noise Ratio Calculator

Other calculators ...

Free statistical calculators, comparison of means calculator, description.

This procedure calculates the difference between the observed means in two independent samples. A significance value (P-value) and 95% Confidence Interval (CI) of the difference is reported. The P-value is the probability of obtaining the observed difference between the samples if the null hypothesis were true. The null hypothesis is the hypothesis that the difference is 0.

Required input

Computational notes.

The standard error se of the difference between the two means is calculated as:

The P-value is the area of the t distribution with n 1 + n 2 − 2 degrees of freedom, that falls outside ± t (see Values of the t distribution table).

When the P-value is less than 0.05 (P<0.05), the conclusion is that the two means are significantly different. Note that in MedCalc P-values are always two-sided (or two-tailed).

How to cite this page

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

POPULAR USE CASES

INTEGRATIONS

T test calculator

A t test compares the means of two groups. There are several types of two sample t tests and this calculator focuses on the three most common: unpaired, welch's, and paired t tests. Directions for using the calculator are listed below, along with more information about two sample t tests and help on which is appropriate for your analysis. NOTE: This is not the same as a one sample t test; for that, you need this One sample t test calculator .

1. Choose data entry format

Caution: Changing format will erase your data.

2. Choose a test

Help me choose

3. Enter data

Help me arrange the data

4. View the results

What is a t test.

A t test is used to measure the difference between exactly two means. Its focus is on the same numeric data variable rather than counts or correlations between multiple variables. If you are taking the average of a sample of measurements, t tests are the most commonly used method to evaluate that data. It is particularly useful for small samples of less than 30 observations. For example, you might compare whether systolic blood pressure differs between a control and treated group, between men and women, or any other two groups.

This calculator uses a two-sample t test, which compares two datasets to see if their means are statistically different. That is different from a one sample t test , which compares the mean of your sample to some proposed theoretical value.

The most general formula for a t test is composed of two means (M1 and M2) and the overall standard error (SE) of the two samples:

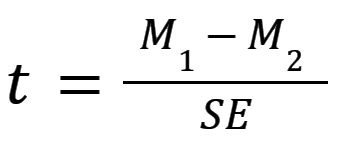
See our video on How to Perform a Two-sample t test for an intuitive explanation of t tests and an example.

How to use the t test calculator

• Choose your data entry format . This will change how section 3 on the page looks. The first two options are for entering your data points themselves, either manually or by copy & paste. The last two are for entering the means for each group, along with the number of observations (N) and either the standard error of that mean (SEM) or standard deviation of the dataset (SD) standard error. If you have already calculated these summary statistics, the latter options will save you time.
• Choose a test from the three options: Unpaired t test, Welch's unpaired t test, or Paired t test. Use our Ultimate Guide to t tests if you are unsure which is appropriate, as it includes a section on "How do I know which t test to use?". Notice not all options are available if you enter means only.
• Enter data for the test, based on the format you chose in Step 1.
• Click Calculate Now and View the results. All options will perform a two-tailed test .

Performing t tests? We can help.

Sign up for more information on how to perform t tests and other common statistical analyses.

Common t test confusion

In addition to the number of t test options, t tests are often confused with completely different techniques as well. Here's how to keep them all straight.

Correlation and regression are used to measure how much two factors move together. While t tests are part of regression analysis, they are focused on only one factor by comparing means in different samples.

ANOVA is used for comparing means across three or more total groups. In contrast, t tests compare means between exactly two groups.

Finally, contingency tables compare counts of observations within groups rather than a calculated average. Since t tests compare means of continuous variable between groups, contingency tables use methods such as chi square instead of t tests.

Assumptions of t tests

Because there are several versions of t tests, it's important to check the assumptions to figure out which is best suited for your project. Here are our analysis checklists for unpaired t tests and paired t tests , which are the two most common. These (and the ultimate guide to t tests ) go into detail on the basic assumptions underlying any t test:

• Exactly two groups
• Sample is normally distributed
• Independent observations
• Unequal or equal variance?
• Paired or unpaired data?

Interpreting results

The three different options for t tests have slightly different interpretations, but they all hinge on hypothesis testing and P values. You need to select a significance threshold for your P value (often 0.05) before doing the test.

While P values can be easy to misinterpret , they are the most commonly used method to evaluate whether there is evidence of a difference between the sample of data collected and the null hypothesis. Once you have run the correct t test, look at the resulting P value. If the test result is less than your threshold, you have enough evidence to conclude that the data are significantly different.

If the test result is larger or equal to your threshold, you cannot conclude that there is a difference. However, you cannot conclude that there was definitively no difference either. It's possible that a dataset with more observations would have resulted in a different conclusion.

Depending on the test you run, you may see other statistics that were used to calculate the P value, including the mean difference, t statistic, degrees of freedom, and standard error. The confidence interval and a review of your dataset is given as well on the results page.

Graphing t tests

This calculator does not provide a chart or graph of t tests, however, graphing is an important part of analysis because it can help explain the results of the t test and highlight any potential outliers. See our Prism guide for some graphing tips for both unpaired and paired t tests.

Prism is built for customized, publication quality graphics and charts. For t tests we recommend simply plotting the datapoints themselves and the mean, or an estimation plot . Another popular approach is to use a violin plot, like those available in Prism.

For more information

Our ultimate guide to t tests includes examples, links, and intuitive explanations on the subject. It is quite simply the best place to start if you're looking for more about t tests!

If you enjoyed this calculator, you will love using Prism for analysis. Take a free 30-day trial to do more with your data, such as:

• Clear guidance to pick the right t test and detailed results summaries
• Custom, publication quality t test graphics, violin plots, and more
• More t test options, including normality testing as well as nested and multiple t tests
• Non-parametric test alternatives such as Wilcoxon, Mann-Whitney, and Kolmogorov-Smirnov

Check out our video on how to perform a t test in Prism , for an example from start to finish!

Remember, this page is just for two sample t tests. If you only have one sample, you need to use this calculator instead.

We Recommend:

Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required.

Two sample t test calculator

Welcome to our Two Sample T Test Calculator, the ideal tool for comparing mean values from two independent samples. This calculator calculates test statistics, p-values, critical values, judgments, and conclusions using both equal and unequal variance approaches. This tool is intended to help students, researchers, and data analysts simplify their statistical analyses.

Enter below values for sample 1 :

Enter below values for sample 2:

Related Calculators :

• List of all calculator
• P-value calculator
• Critical value Calculator

What is a Two Sample T Test?

A Two Sample T Test is used to see if there is a significant difference in the means of two independent groups. This test is frequently used in experiments and research to compare two groups and draw conclusions about the population mean.

Features of Our Two Sample T-Test Calculator

• Direct Data Entry: Enter each sample's raw data values directly into the calculator.
• Summary Statistics: If you have summary statistics rather than raw data, please provide the sample size, mean, and standard deviation.
• Hypothesis Testing: Determine whether your null and alternative hypotheses are two-tailed, right-tailed, or left-tailed.
• Significance Level: Enter the significance level (alpha) for the test.
• Variance Type: For more accurate results, select either equal or unequal variance.
• Detailed Results: Receive complete results, including test statistics, p-values, critical values, and decision-making conclusions.

How To Use The Calculator

Select Data Type: Determine whether you have raw data values or summary statistics.

Enter Data: Fill in the data values or summary statistics for both samples.

Hypothesis Selection: Determine the relevant null and alternative hypotheses for your test.

Set the Significance Level: The alpha level is used to set the threshold for statistical significance.

Variance Type: Determine whether the variances of the two samples are equal or unequal.

Calculate: To view the results, simply click the "Calculate" button.

Example Use Cases

Our Two Sample T-Test Calculator can be applied in various fields, including:

• Medical Research: Determine the efficacy of two different drugs.
• Education: Compare test scores from two distinct teaching approaches.
• Marketing: Evaluate the effectiveness of two marketing efforts.

Why Use Our Calculator?

• Accuracy: Our calculator can perform precise estimates for both equal and unequal variance cases.
• Ease of Use: A user-friendly interface with clear directions and inputs.
• Comprehensive Results: Detailed output, including statistical computations and decision-making advice.

Frequently Asked Questions

Q: What is the difference between equal and unequal variances? A: Equal variance assumes that the two populations have equal variance, whereas unequal variance does not make this assumption. Selecting the proper option guarantees accurate results.

Q: How do I determine whether to conduct a two-tailed, right-tailed, or left-tailed test? A: It depends on your research hypothesis. If you want to find a significant difference, conduct a two-tailed test. If you predict the first sample's mean to be greater than the second, perform a right-tailed test. If you predict the first sample's mean to be less than the second, perform a left-tailed test.

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

T-Test Calculator for 2 Independent Means

This simple t -test calculator, provides full details of the t-test calculation, including sample mean, sum of squares and standard deviation.

Further Information

A t -test is used when you're looking at a numerical variable - for example, height - and then comparing the averages of two separate populations or groups (e.g., males and females).

Requirements

• Two independent samples
• Data should be normally distributed
• The two samples should have the same variance

Null Hypothesis

H0: u1 - u2 = 0, where u1 is the mean of first population and u2 the mean of the second.

As above, the null hypothesis tends to be that there is no difference between the means of the two populations; or, more formally, that the difference is zero (so, for example, that there is no difference between the average heights of two populations of males and females).