research paper bond market

Factor-based investing in government bond markets: a survey of the current state of research

• Original Article
• Open access
• Published: 11 March 2020
• Volume 21 , pages 94–105, ( 2020 )

Cite this article

You have full access to this open access article

• Demir Bektić   ORCID: orcid.org/0000-0002-8887-3521 1 , 3 ,
• Britta Hachenberg 2 &
• Dirk Schiereck 3  

4974 Accesses

5 Citations

Explore all metrics

A Correction to this article was published on 29 September 2021

This article has been updated

Factor investing has become very popular during the last decades, especially with respect to equity markets. After extending Fama–French factors to corporate bond markets, recent research more often concentrates on the government bond space and reveals that there is indeed clear empirical evidence for the existence of significant government bond factors. Voices that state the opposite refer to outdated data samples. By the documentation of rather homogeneous recent empirical evidence, this review underlines the attractiveness of more sophisticated investment approaches, which are well established in equity and even in corporate bond markets, to the segment of government bonds.

Similar content being viewed by others

Multifactor Portfolio Construction by Factor Risk Parity Strategies: An Empirical Comparison of Global Stock Markets

Relative value in corporate bond sectors, the q -factor model and the redundancy of the value factor: an application to hedge funds.

Avoid common mistakes on your manuscript.

Introduction

The still fast-growing body of the literature which concentrates on the predictability of variations in international asset returns has a clear focus on equity markets where more than 300 papers on cross-sectional returns are counted (Crawford et al. 2019 ; Harvey et al. 2016 ). Barr and Priestley ( 2004 ) argue that it is reasonable to expect equity markets to be less closely integrated than bond markets, largely because differences between bonds in different countries are small. However, Bektić et al. ( 2019 ) and Dekker et al. ( 2019 ) provide convincing evidence for the explanatory power of the Fama–French factors also in corporate bond markets. Additionally, Houweling and van Zundert ( 2017 ), Bektić ( 2018 , 2019 ) as well as Israel et al. ( 2018 ) show that further well-known factors from equity markets could be translated to corporate bonds. These findings are consistent to early results by Harvey et al. ( 1994 ) who show that factors driving bond returns are the same as those driving equity returns.

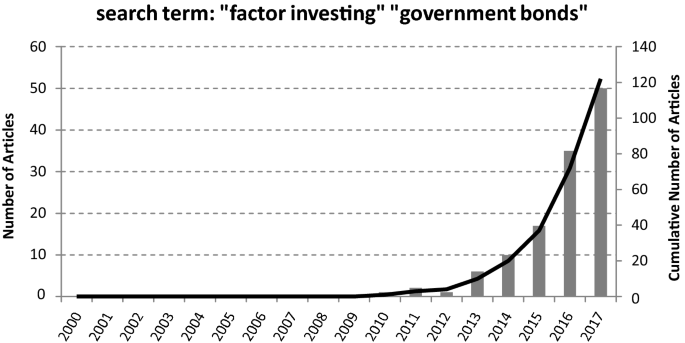
Compared to these two asset classes, research on government bond Footnote 1 return factors was perceived as less attractive because excess returns of long-term government bonds are subject only to interest rate risk in the absence of default risk and cash flow uncertainty (Ilmanen 1995 ). Besides approaches to explain predictable variation in government bond returns with measures of time-varying risk (Lauterbach 1989 ; Boudoukh 1993 ), more technical factors were tested. In this context, Litterman and Scheinkman ( 1991 ) support the idea of identifying common factors that affect the returns on US government bonds and related factors. They provide evidence that three attributes of the yield curve—level, steepness and curvature—can explain returns on all fixed-income securities. However, in recent years a number of papers have extended the idea of factor investing from the corporate bond market to the government bond market, and by doing so, they also address the increasing demand for insights in this area as shown in Figs.  1 and 2 .

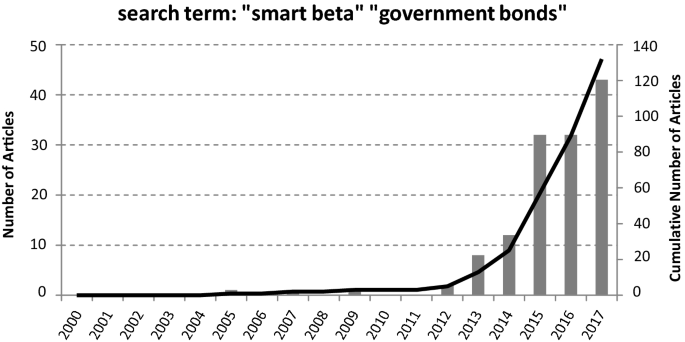
Number of articles found via Google Scholar for the period from December 2000 until December 2017

These impressive demand patterns are interpreted as a perceived lack of structured overall survey information on the state of research on factor-based investing in government bond markets. We address this research gap and intend to give an overview on factors in government bond markets. These factors are often defined as investments that produce long-term returns using risk factors that are significant and unique, in the sense that they are not subsumed by other traditional risk factors. Such investment strategies are usually applied in a long–short or long-only (smart beta) manner. However, while the most popular applications of these factors are dedicated to the equity market, the extension of risk factors to non-equity markets has been an important trigger for empirical research in the modern asset pricing literature. Footnote 2

As the underlying asset classes of equity and sovereign bond markets are fundamentally different, so are the implications for investors seeking to track portfolios versus market capitalization-weighted benchmarks for each asset class, as well. On the one hand, while both equity and fixed-income benchmarks contain a large number of securities, constituents of fixed-income indices are usually changing due to the maturing nature of fixed-income securities. On the other hand, while market capitalization-weighted equity benchmarks enable investors to hold mean variance efficient portfolios, market capitalization-weighted indices in the bond market force investors into the most prolific issuers of debt, which intuitively are associated with elevated levels of risk. This counterintuitive dynamic of market capitalization-weighted indices in bond markets is known as the “bums problem” (Siegel 2003 ) and, in terms of government bonds, leads to assigning the largest weight to those countries with the largest amounts outstanding in the index. These dynamics in fixed-income markets motivate why factor-based strategies may significantly and sustainably outperform their market capitalization-weighted peers. For instance, Ilmanen et al. ( 2019 ) analyze a century of data across six asset classes and find significant time variation in single-factor returns and variances, providing support for models of dynamic return premia and, at the same time, rejecting models of macroeconomic risks, which were perceived to have predictive power in the past. Footnote 3

The focus of our article is on the five best documented and most cited factors, namely momentum, value, quality (defensive), carry and liquidity. We compare and analyze different factor definitions as well as data sets which are used to conduct the corresponding research. Finally, we show how investors should pursue factor strategies to generate significantly higher risk-adjusted returns as well as to further diversify their portfolios.

Momentum is probably one of the most popular factors in equity markets. In short, momentum is the tendency for an asset’s recent performance to continue in the short term (Brooks et al. 2018 ). Hamdan et al. ( 2016 ) also discuss that a risk factor is not necessarily a risk premium. A momentum strategy follows the market, and in trend-following strategies, there is no additional exposure to a risk during “bad” times. Thus, they argue that momentum is a risk factor and a market anomaly instead of a risk premium. This trend-following definition is also used by Brightman and Shepherd ( 2016 ). They note that intuitively this might seem to violate the efficient market hypothesis; however, empirical results show that momentum is a robust strategy even across asset classes.

For instance, Asness et al. ( 2013 ) show that momentum exists in every major asset class. They employ a simple measure of momentum, the past 12-month cumulative raw return not including the most recent month. Their momentum portfolios are constructed as long-only as well as long–short portfolios where securities are weighted according to their signal rank. Additionally, Brightman and Shepherd ( 2016 ) use each country’s own historical return in a time series approach and report statistically significant Sharpe ratios and mean returns based on momentum in government bond markets.

Another important finding from Asness et al. ( 2013 ) is the negative correlation of value and momentum. This creates a significant diversification effect on their 50/50 portfolio consisting of value and momentum tilts and leads to stronger results. The negative correlation also can be observed through the first principle component and the liquidity risk’s loadings on value and momentum. They argue that the negative relation between value and momentum might be the result of their opposite sign loadings on liquidity risk as value loads negatively, while momentum loads positively on liquidity. This positive loading on liquidity indeed captures to some extent the variation in momentum returns.

Similar to Asness et al. ( 2013 ), Brooks et al. ( 2018 ) define momentum as each country’s own 12-month average excess return. They show that the long-only tercile portfolios exhibit positive results, while the long–short alpha is not statistically significant. Additionally, these authors construct a multifactor (COMBO) portfolio and show that momentum has a negative correlation with value, carry and quality for government bonds (− 0.32, − 0.42 and − 0.22). Therefore, investors can exploit significant diversification benefits when combining factors rather than employing just one single factor in a portfolio (COMBO portfolio alpha = 2.8%, t -stat = 3.89). The negative correlation of − 0.18 between momentum and value is also observed in Brightman and Shepherd ( 2016 ).

Brooks and Moskowitz ( 2017 ) explore momentum in the cross section across countries using level, slope and curvature portfolios, which is a novel approach. In the cross section of government-level returns, momentum is an insignificant factor (duration-adjusted). Unlike carry and value, it also does not capture any information from principal components. In the cross section of country slope returns, momentum again is not a significant factor and not related to any principal component. It only becomes significant when principal components and carry are added to the regression, but its coefficient is negative. Principal components can explain only 25.5% and 40.7% of cross-sectional and time series variation of momentum in slope strategies. This drops even further for level strategies, but remains important for curvature strategies in a time series analysis. When curvature is high, recent returns of intermediate bonds are lower compared to the bonds at the longer end of the curve. This can be observed in the correlation structure of momentum which is negatively correlated with the third principal component (related to the curvature).

Brooks and Moskowitz ( 2017 ) also examine the performance of factors using traded bond data from J.P. Morgan across level, slope and curvature portfolios. In level portfolios, momentum delivers 5.02% alpha ( t -stat = 2.46) when the principal components are included in the regression. Additionally, momentum is negatively correlated with the first principal component as well as value across level, slope and curvature portfolios (− 0.36, − 0.13 and − 0.51, respectively). These results indeed indicate that momentum is a unique factor in level portfolios and is not captured by other known factors.

Since principle components are not sufficient to explain the variation in momentum, further unspanned factors are examined as well. For instance, momentum has a negative coefficient for macroeconomic variables (growth and inflation), although they are not significant. The relation to the Cochrane and Piazessi ( 2005 ) factor is tested only by using level time-varying portfolios where momentum is negative and significant. Brooks et al. ( 2018 ) as well study the exposures to macroeconomic factors (growth, inflation, real yield, volatility and illiquidity) but only for long–short portfolios. However, we can conclude that government bond portfolios based on factors have less sensitivity to shocks in macroeconomic variables than common sovereign bond indices.

Finally, Brooks and Moskowitz ( 2017 ) compare government bond factors with factors from other asset classes. For instance, level momentum is positively correlated across asset classes and the correlation is significant with momentum in currency and commodity markets.

These findings indicate that momentum can be an important factor across asset classes as it has a significant positive loading on equity momentum as well which is also confirmed by the study of Brightman and Shepherd ( 2016 ). Furthermore, Durham ( 2015 ) shows that momentum produces meaningfully alphas in the US Treasury market. Table  1 summarizes the studies discussed above.

Value is a widely known equity market factor and one of the most studied ones across asset classes. In short, it is the tendency for relatively cheap assets to outperform relatively expensive assets (Brooks et al. 2018 ). Asness et al. ( 2013 ) test value across different asset classes and employ a simple and standard definition for equity markets (asset’s book value relative to its current market value). Furthermore, a similar approach is extended to government bonds using the 5-year change in the yields of 10-year bonds. This definition is similar to the negative of the past 5-year return which is shown to have a high correlation with the value factor using book-to-market equity ratios (see Fama and French, 1996 ). They also analyze value using alternative measures, such as real bond yield and term spread. Footnote 4

Mazzoleni and Kunz ( 2018 ) use two different measures of value (real bond yield as defined by Asness et al. ( 2013 ) and the term spread) and create two portfolios accordingly. In the period between March 1989 and October 2017, the term spread portfolio produces a 3.4% return with a 0.47 Sharpe ratio, while the real yield portfolio has a mean return of − 0.7%. It should be noted that the returns used to calculate these results are based on the 10-year Treasury bonds and the US cash rate. They further investigate the positive return in their term spread portfolio by dividing the total return into two components; carry return and spot return using the Koijen et al. ( 2018 ) carry definition. The results show that nearly half of the return on the term spread portfolio can be captured by carry, and the term spread value is positively correlated with carry.

They also apply these two definitions to global government bonds and construct long–short portfolios (a long position in the top third and a short position in the bottom third of the universe). The global term spread portfolio and the global real yield portfolio produce 1.1% return (Sharpe ratio = 0.49) and 0.5% return (Sharpe ratio = 0.26), respectively. The global term spread and real yield bond value portfolios are negatively correlated (− 0.33).

In order to explain the variation observed in value, Asness et al. ( 2013 ) investigate common macroeconomic and liquidity risk factors. The macroeconomic factors are regressed on a portfolio consisting of all the non-stock assets; hence, a more reliable variation effect may be captured when testing on global government bonds only. In general, they also find that global funding liquidity shocks have negative impact on value returns. This may be partly due to the price pressure the flight-to-liquidity trades create when a shock occurs. However, the exposure of value returns in global government bonds to liquidity risks is weak.

Brooks et al. ( 2018 ) employ a value measure in government bonds, where the real bond yield is calculated by comparing nominal yields versus maturity-matched inflation expectations. The global government bond data and the portfolio construction method (tercile long-only portfolios and long–short duration-neutral portfolios) are the same as previously described in the momentum section above. When their value definition is applied across countries, the return pattern shows that countries with relatively high yields are preferred. Additionally, the Sharpe ratio improves from the low value to the high-value tercile portfolio (0.87 to 1.07). For the long–short portfolio, value produces a significant and positive alpha (2.02%) with a Sharpe ratio of 0.65.

Brooks and Moskowitz ( 2017 ) analyze the relationship between value and common bond market factors. They also employ the real bond yield as a measure of value and their strategy performs when the level of yields reverts to expected inflation (which is the maturity-matched CPI inflation forecast). The excess return of level portfolios across countries is regressed on value and the coefficient is 0.53 ( t -stat = 3.56). The value factor even increases its significance when carry and momentum are added to the regression ( t -stat = 3.72). This finding seems to strengthen the hypothesis that value and other known factors are orthogonal to each other, harvesting different sources of return. Additionally, value remains significant when principal components are included in the regression as well.

Brooks and Moskowitz ( 2017 ) find that the first principal component (PC1), which is highly related to “level” of the yield curve, becomes insignificant in the presence of value ( t -stat drops 2.63 to 1.05). Value also loads positively on PC1 when level-neutral long–short portfolios are employed. The regression is repeated for slope and curvature portfolios across countries. Finally, a long–short value portfolio consisting of level, slope and curvature portfolios, weighted according to the inverse of volatility, exhibits a statistically significant alpha with a Sharpe ratio of 0.95.

To better understand the power of value in explaining the returns of government bonds, other macrofactors such as growth in industrial production and inflation for each country are added to the regressions of level, slope and curvature portfolios. While macrofactors do not capture any information in slope and curvature portfolios, interesting results are observed in level portfolios. Here, value remains significant when the returns are controlled for macrofactors and principal components, but the previously significant inflation factor is now subsumed by value. Footnote 5

Finally, Brooks and Moskowitz ( 2017 ) show that the value factor in level portfolios is positively related to and correlated with value strategies in other asset classes like equities and currencies. The co-movement of value strategies is also documented by Asness et al. ( 2013 ). Additionally, Brightman and Shepherd ( 2016 ) and Mazzoleni and Kunz ( 2018 ) also find supporting evidence for this finding by showing that value in bonds is correlated with value in currencies and equities (0.20 and 0.25). Therefore, value seems to be a significant and important factor across asset classes and as a result should be an integral component of a government bond portfolio as well. Table  2 summarizes the above-discussed studies.

Quality (defensive)

The economic intuition behind a defensive strategy can be summarized as the tendency of low-risk assets to deliver higher risk-adjusted returns compared to assets with higher risk and consists of buying low-beta assets while selling high-beta assets (Brooks et al. 2018 ).

Brooks et al. ( 2018 ) employ effective duration as their low-risk measure and apply the defensive strategy across maturities unlike other style factors which are investigated across countries. Since the defensive strategy uses duration as the fundamental measure of the quality factor, it prefers shorter maturities across all countries. They construct equally weighted portfolios containing the short maturity bucket across all countries in the top tercile and long maturity buckets in the bottom tercile. The top minus bottom duration-neutral tercile portfolio goes long on short maturities while taking a short position on higher maturity securities. The resulting mean returns of the long-only defensive strategy are positive and decrease monotonically from the top to the bottom tercile portfolio. The long–short defensive portfolio produces a significant alpha as well (1.3%, t -stat = 2.18). Furthermore, the factor also exhibits a low positive correlation with value and carry (0.21 and 0.15) and is negatively correlated with momentum (− 0.22). Thus, it amplifies the diversification benefits when constructing multifactor portfolios.

As already stated in the introduction, a meaningful risk factor should gain a return that cannot be obtained by exposure to other factors. Hence, Brooks et al. ( 2018 ) run regressions where the long–short defensive portfolio returns are regressed on traditional market risk premia as well as equity factor premia. However, the defensive factor produces statistically significant alphas even when controlled for these additional factor exposures.

Another adoption of the defensive strategy is the betting against beta (BAB) approach introduced by Frazzini and Pedersen ( 2014 ). This strategy is based on a similar hypothesis that high-risk assets offer lower returns compared to low-risk assets when adjusted for risk. The strategy first sorts assets ranked by their beta value and then short-sells the high-beta assets while taking a long position on the low-beta assets. However, these low-risk assets often require leverage as the portfolio maintains market neutrality (see Asness et al. 2015 ).

Frazzini and Pedersen ( 2014 ) also extend their BAB strategy to government bonds. The data are obtained from the Center for Research in Security Prices (CRSP) US Treasury Database and ranges from January 1952 to March 2012. To calculate beta, they use equally weighted portfolios consisting of all the bonds in the index. Then, to create the BAB bond factor, they go long the shorter maturity bonds (as leveraged low-beta bonds) and short the longer term bonds (as de-leveraged high-beta bonds). The obtained BAB portfolio delivers a significant Sharpe ratio of 0.81 ( t -stat = 6.26), and the results remain almost unchanged when time-varying market exposure is included in the regression analysis.

Finally, Frazzini and Pedersen ( 2014 ) note that BAB bond portfolios may be subject to funding constraints as investors would need a high level of leverage to implement such a strategy in practice. Hence, this trade depends on the individual leverage constraints of each investor.

However, Durham ( 2018 ) shows that investors should follow such a strategy cautiously as it seems to be associated with substantial systematic risk. Table  3 summarizes the studies discussed above.

Koijen et al. ( 2018 ) define bond carry as the return on a government bond when the yield curve does not change during the holding period. The main reason for its popularity in fixed income is that it is quick and easy to calculate. The predominantly employed definition specifies carry as an asset’s future (or synthetic) return, assuming that interest rates remain unchanged over time. Hamdan et al. ( 2016 ) state that “the underlying idea of a carry strategy is to capture a spread or a return by betting that the underlying risk will not occur or that market conditions will stay the same” (p. 21).

Koijen et al. ( 2018 ) adapt this definition for government bonds by relating carry to the slope of the yield curve and by adding the “roll down” component that captures the price change which occurs as the bond moves along the yield curve as time passes. Thus, the carry strategy in general is defined as taking a long position on high carry assets and a short position on low carry assets. Furthermore, Koijen et al. ( 2018 ) note that the application in global government bond markets is even easier when bond futures are employed to implement the strategy. However, liquid bond futures contracts are only available in a small number of countries. Thus, they use synthetic futures prices to test the application of carry in the cross section of global government bonds. Based on their definition, it is easy to see the connection between bond carry and forward rates. Additionally, when modified duration is included, carry can be separated into two effects: the bond’s yield spreads to the risk-free rate and the price appreciation of the bond as it moves on the yield curve. To account for different duration exposures between global government bonds, they use a duration-adjusted position sizing.

The data set of Koijen et al. ( 2018 ) includes 10 countries starting from November 1983 till September 2012, and the returns are calculated by using the 10-year minus 2-year slope returns in each of the 10 markets. Additionally, they also analyze the 10-year global yields based on the level of the yield curve. Then, the carry returns of global government bond portfolios are regressed on the corresponding bond market returns, the global value and momentum bond factors, as well as the time series bond momentum as defined by Moskowitz et al. ( 2012 ), to understand what is actually behind the variation in carry returns. The resulting alphas are positive and statistically significant. Hence, carry strategies deliver excess returns in each country without a significant exposure to the corresponding bond market. The alpha remains significantly positive when tested against cross-sectional and time series momentum. Further tests analyze the relation between global carry returns and downside risk where the returns are positively exposed to global liquidity shocks and negatively exposed to volatility risk except for the US Treasuries where this relationship is the other way round. However, the alphas of the carry strategy in global government bonds and Treasuries are statistically significant. Therefore, to explain the cross section of government bond carry strategy returns, risk premia and exposure to the above-mentioned risk factors are not a sufficient explanation.

Similar to Koijen et al. ( 2018 ), Brooks et al. ( 2018 ) define carry as the tendency for higher-yielding assets to outperform lower-yielding assets and summarize it as the reaching for yield . Brooks et al. ( 2018 ) use a sample of government bonds consisting of all the bonds from the J.P. Morgan Government Bond Index (13 markets in total) and divide them into three maturity buckets (1–5-year, 5–10-year and 10–30-year bucket). Then, they test carry by taking an equal duration-weighted average across the three maturity buckets within each country. The sample period for both long-only tercile portfolios and long–short portfolios is from January 1996 to June 2017. Finally, Brooks et al. ( 2018 ), Koijen et al. ( 2018 ) and Brightman and Shepherd ( 2016 ) report similar Sharpe ratios.

Brooks et al. ( 2018 ) also test whether the premium captured by a carry strategy is unique to factor investing or whether it can be earned through investing in well-known risk premia such as (1) the credit risk premium, (2) the equity risk premium and (3) the bond term premium as well as dynamic factors such as size, value and momentum. They document only small exposure to both the credit risk premium and the bond term premium, and a small but negative exposure to size. However, the R2 of the regression is only 8% which indicates that these risk premia cannot explain the return variability in government bonds. The authors also investigate the sensitivities of long–short government bond portfolios to shocks in macroeconomic and financial conditions. They use quarterly data of growth, inflation, real yield, volatility and illiquidity between January 1997 and June 2017. However, the patterns for government bond carry portfolios are significantly more stable compared to the market as they show little sensitivity to macroeconomic or financial market shocks.

Beekhuizen et al. ( 2019 ) improve the betting against beta (BAB) results of Frazzini and Pedersen ( 2014 ) by using a duration-neutral portfolio instead of a beta-neutral portfolio. An interesting result is that curve carry still performs with a significant alpha when BAB is added as an explanatory variable in the regression although it loads heavily on BAB. The authors believe that this is the result of both strategies having a preference for lower-maturity buckets in times of lower funding rates. However, the reverse regression shows that BAB does not add value beyond curve carry, claiming curve carry a superior strategy.

Brooks and Moskowitz ( 2017 ) find that carry subsumes the explanatory power of the slope and the curvature of the yield curve. They investigate both the time series and the cross-sectional performance of international government bonds’ returns in the level, slope and curvature of the yield curve. The level and slope portfolios are built similar to Koijen et al. ( 2018 ), using 10-year bond yields and the difference of 10- and 2-year bond yields, respectively. They also include the “butterfly” portfolio where they use the difference between the 5- and an average of the 2- and 10-year bonds. The results for level portfolios in the cross section show that carry is mostly related to the second principal component (PC2). Furthermore, the univariate forecasting regression results show that carry captures significant and positive risk premia in the cross section of government bond-level returns (0.25%; t -stat = 2.11). In slope portfolios, carry is adjusted for duration to make the results more reliable. However, carry still produces significantly positive returns and becomes a stronger return predictor for slope portfolios compared to level portfolios. Similar results are obtained for the butterfly returns across countries for carry as it generates a significant and positive alpha. Additionally, the authors also examine the time variation in expected returns of the level, slope and butterfly portfolios of each country and the results confirm the findings from the cross-sectional analysis. Finally, the results show that carry continues to exhibit a significant positive alpha even when macrofactors like one-year-ahead forecasts of inflation and industrial production growth are included in the asset pricing tests. Footnote 6

Brooks and Moskowitz ( 2017 ) also show that both the carry returns of the time variation and the cross section of the level portfolios are positively related to carry returns of equity indices, currencies and global bond indices. Additionally, Brightman and Shepherd ( 2016 ) also document a positive correlation of bond carry with equity and currency carry, and a negative correlation with commodity carry. Lastly, Hamdan et al. ( 2016 ) state that a carry strategy is betting that the forward price is not a true estimator of the spot price and it goes against the financial theory of rational expectations. Therefore, both Brooks and Moskowitz ( 2017 ) and Hamdan et al. ( 2016 ) state that carry strategies become extremely risky during market distress mostly due to their higher probability of drawdowns. Table  4 summarizes the above-discussed studies.

Government bond yields are heavily affected by the indebtedness of the particular government; thus, a liquidity premia in government bond markets should be observed. Bernoth et al. ( 2004 ) argue that the liquidity component of the yield spreads highlights a lack of financial market integration. They disintegrate the equation of bond yield difference between two bonds into three segments where one of them is the liquidity risk premium. Intuitively, the liquidity risk premium increases when the domestic bond market decreases in liquidity. Besides the basic model, Bernoth et al. ( 2004 ) test the liquidity variable in a reduced form model as well for 13 European Union (EU) government bond markets between 1991 and 2002. Footnote 7 In this model, they use the positive correlation between liquidity and the total supply of debt (see Gravelle 1999 ) and assume that the liquidity premium should be proportional to the ratio of the debt issued by a government to the total debt of the European Union issued in Deutsche Mark or euro and US dollars. They show that the liquidity risk premium is larger for USD denominated bonds. Finally, they observe that the effect of EU membership on liquidity is positive as the coefficient of liquidity turns from negative to positive in all regressions when a country becomes a member of the EU. This finding indicates that with EU membership, financial market integration across countries increases and members therefore exhibit a lower-liquidity-risk premium.

Favero et al. ( 2010 ) investigate the liquidity effect and how it is priced in the EU area as well. The popularity of the EU area in academia for researchers concerning liquidity comes from the elimination of exchange rate risk in bonds and the bonds from different countries’ not being a substitute for each other as they still show some variation. This variation indicates that different sovereign countries in the EU have different risk profiles.

Favero et al. ( 2010 ) develop an asset pricing model with an endogenous liquidity premium variable. The model assumes that trading costs and the availability of other investments in the market affect the liquidity premium. They believe that the liquidity premium decreases when the aggregate market risk increases. This assumption contradicts with other studies in the literature supporting the notion that an increase in volatility increases the liquidity premium as investors usually want to liquidate their asset in times of market turmoil (flight-to-liquidity). They argue that if the illiquidity and the volatility increase at the same time, asset prices would increase, while the positive change in their return would decrease. The authors conclude that this effect comes from the interaction between liquidity and aggregate market risk. Hence, the liquidity risk premium exists in government bond markets and the yield differentials depend on the interaction between the liquidity variable and the exposure to aggregate risk.

Boudoukh et al. ( 2016 ) show that if a bond’s liquidity increases, the price of that bond decreases. They analyze the liquidity effect in 10 sovereign bond markets (developed countries) over a 17-year period by comparing newly issued bonds to the most recent previously issued bonds.

Intuitively, during times of market turmoil, we would expect investors to prefer more liquid assets and the spread between newly issued government bonds and the previously issued ones to widen. However, their results show that in “bad” times, the newly issued spread actually tightens and becomes negative in those countries with relatively lower credit quality.

Ejsing et al. ( 2012 ) investigate the liquidity premium as well and how it is connected with the flight-to-quality phenomenon, especially during the 2008 financial crisis and subsequent sovereign debt crisis. In contrast to other studies, they focus solely on the highly rated and liquid France and Germany government bonds and they measure the liquidity premia as the difference in the term structures of government guaranteed agency bonds over government bonds. The data set includes daily bond prices of the German Kreditanstalt für Wiederaufbau (KfW) and the French Caisse d’Amortissement de la Dette Sociale (CADES), as well as the German and French government bonds (obtained from Bloomberg for the period from January 2006 to October 2011) to calculate the corresponding yield curves.

The increase in liquidity of German/French government and agency bonds is very clear during the 2008/09 financial crisis as well as during the euro area debt crisis. In their model-based framework, they take the liquidity factor as a latent factor of their state–space model. The difference between the two models comes from assuming that the pricing of liquidity can also affect agency yields. The estimation results show that the liquidity premium in agency yields can explain 30% of the variation in the agency–government yield spread. The results also show that in times of crises, both German and French yields suffered due to an increased demand for highly rated assets. Therefore, this paper also presents evidence on the flight-to-quality effect and shows why liquidity plays an important role in investors’ portfolios. Table  5 summarizes the studies discussed above.

The concept of factor-based investing in the fixed-income space is still relatively less mature compared to equities, despite the obvious importance and relevance of the subject, and can for certain no longer be denied by looking at current figures. Especially in times of possible rising rates in a low-yield environment, new approaches to fixed-income investing have sparked investors’ interest. In this review, we therefore clearly state that factor investing in sovereign bond markets represents a new paradigm for a holistic portfolio construction process.

The traditional market capitalization-weighted approach has often been criticized for its lack of diversification, especially in bond markets. It is questionable at best if fixed-income indices, in the way they are constructed, are representing what they are supposed to do as the level of indebtedness is not necessarily representative for the market as a whole. Therefore, factors like momentum, value, quality, carry and liquidity should not be neglected when constructing fixed-income portfolios as we observe strong support for the existence of significant factors in global government bond markets. Moreover, based on a review of the literature, all examined factor strategies generate a significant alpha.

While the corresponding positive returns can be captured through investing in each factor individually, employing multifactor portfolios produces more persistent and even higher risk-adjusted returns. This is mainly due to the low correlation between factors as well as due to different market behavior of each factor across the business cycle. Therefore, multifactor portfolios provide better and a more efficient diversification. However, not only the implemented strategy and factor definition preferences but also the specific implementation design like investment universe as well as rebalancing frequency, transaction costs, weighting scheme and definition of portfolio configuration has a significant impact on performance and explains why two portfolios (or funds) based on seemingly identical factors may perform differently. Additionally, from our review of the literature, it is not always clear whether currency risk is hedged or left unhedged. As currency moves and hence volatility can be substantial, especially in the short term, significant differences in performance between hedged and unhedged government bond portfolios can occur.

The main criticism of factor outperformance versus conventional benchmarks points at a higher risk exposure to duration and carry trade risk. However, as shown in our literature review, the latest studies control for these exposures and document that the results remain almost unchanged. Additionally, when analyzing alphas of government bond portfolios (or funds) one should also take into account the possibility of omitted risk factors as well as considering investable portfolios. While a theoretical long–short portfolio usually leads to higher risk-adjusted returns, implementing long–short sovereign bond portfolios is complex and non-practical due to operational difficulties and high transaction costs associated with shorting cash bonds, especially for illiquid bonds.

Finally, as already discussed, our examined factors are also employed in other asset classes as well. Therefore, for future research, the adoption of a unified asset pricing model that can be applied across asset classes may be worth considering. Additionally, future research should also examine further significant factors that might impact the performance of government bond markets as this would probably lead to greater financial literacy in this rather underdeveloped field and hence larger investor attention.

Change history

29 september 2021.

A Correction to this paper has been published: https://doi.org/10.1057/s41260-021-00246-w

The terms “sovereign” and “government” bonds are used interchangeably throughout this article.

Traditional approaches in the sovereign bond space primarily included affine term structure models as well as macroeconomic and latent risk factors.

See Ludvigson and Ng ( 2009 ), who provide a summary of macrofactors in bond risk premia.

The term spread is also often used as a sorting variable in carry factor definitions.

The Cochrane and Piazessi ( 2005 ) factor loses its explanatory power as well when value and principal components are present in the regression.

Interestingly, when carry is included in the regression of the time series-level portfolios on the country Cochrane and Piazessi ( 2005 ) factor, this factor is not significant anymore.

Until 1998, they use bonds issued in Deutsche Mark, afterward Euro or USD.

Asness, C., A. Ilmanen, R. Israel, and T. Moskowitz. 2015. Investing with style. Journal of Investment Management 13: 27–63.

Google Scholar  

Asness, C., T. Moskowitz, and L. Pedersen. 2013. Value and momentum everywhere. Journal of Finance 68: 929–985.

Article   Google Scholar  

Barr, D., and R. Priestley. 2004. Expected returns, risk and the integration of international bond markets. Journal of International Money and Finance 23: 71–97.

Beekhuizen, P., J. Duyvesteyn, M. Martens, and C. Zomerdijk. 2019. Carry investing on the yield curve. Financial Analysts Journal 75: 51–63.

Bektić, D. 2018. The low beta anomaly: A corporate bond investor’s perspective. Review of Financial Economics 36: 300–306.

Bektić, D. 2019. Residual equity momentum spillover in global corporate bond markets. Journal of Fixed Income 28: 46–54.

Bektić, D., J.-S. Wenzler, M. Wegener, D. Schiereck, and T. Spielmann. 2019. Extending fama-french factors to corporate bond markets. Journal of Portfolio Management 45: 141–158.

Bernoth, K., J. von Hagen, and L. Schuknecht. 2004. Sovereign risk premia in the european government bond market. Working Paper, ECB Working Paper 369 (June).

Boudoukh, J. 1993. An equilibrium model of nominal bond prices with inflation-output correlation and stochastic volatility. Journal of Money, Credit, and Banking 25: 636–665.

Boudoukh, J., J. Brooks, M. Richardson, and Z. Xu. 2016. The complexity of liquidity: The extraordinary case of sovereign bonds. Working Paper, NBER Working Paper w22576 (August).

Brightman, C., and S. Shepherd. 2016. Systematic global macro. Working Paper, Research Affiliates (December).

Brooks, J., and T. Moskowitz. 2017. Yield curve premia. Working paper, AQR Capital Management, LLC and Yale University, Yale SOM (July). https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2956411 . Accessed Sep 2017.

Brooks, J., D. Palhares, and S. Richardson. 2018. Style investing in fixed income. Journal of Portfolio Management 44: 127–139.

Cochrane, J., and M. Piazessi. 2005. Bond risk premia. American Economic Review 95: 138–160.

Crawford, S., P. Perotti, R. Price, and C.J. Skousen. 2019. Accounting-based anomalies in the bond Market. Financial Analysts Journal 75: 105–124.

Dekker, L., P. Houweling, and F. Muskens. 2019. Factor investing in emerging market credits. Working paper, Tilburg University (November). https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3457127 . Accessed Dec 2019.

Durham, J.B. 2018. Betting against beta with bonds: Worry or love the Steepener? Financial Analysts Journal 72: 57–85.

Durham, J.B. 2015. Can long-only investors use momentum to beat the US treasury market? Financial Analysts Journal 71: 57–74.

Ejsing, J., M. Grothe, and O. Grothe. 2012. Liquidity and credit risk premia in government bond yields. Working Paper, ECB Working Paper 1440 (July).

Fama, E., and K. French. 1996. Multifactor explanations of asset pricing anomalies. Journal of Finance 51: 55–84.

Favero, C., M. Pagano, and E.-L. von Thadden. 2010. How does liquidity affect government bond yields. Journal of Financial and Quantitative Analysis 45: 107–134.

Frazzini, A., and L.H. Pedersen. 2014. Betting against beta. Journal of Financial Economics 111: 1–25.

Gravelle, T. 1999. Liquidity of the government of Canada securities market: Stylized facts and some market microstructure comparisons to the United States treasury market . Working Paper, Bank of Canada Working Paper 99–11 (July).

Hamdan, R., F. Pavlowsky, T. Roncalli, and B. Zheng. 2016. A primer on alternative risk premia . Working paper, Lyxor Asset Management (June).

Harvey, C., B. Solnik, and G. Zhu. 1994. What determines expected international asset returns? Working Paper, NBER Working Paper 4660 (February).

Harvey, C., Y. Liu, and H. Zhu. 2016. …and the cross-section of expected returns. Review of Financial Studies 29: 5–68.

Houweling, P., and J. van Zundert. 2017. Factor investing in the corporate bond market. Financial Analysts Journal 73: 100–115.

Ilmanen, A. 1995. Time-varying expected returns in international bond markets. Journal of Finance 50: 481–506.

Ilmanen, A., R. Israel, T. Moskowitz, A. Thapar, and F. Wang. 2019. Do factor premia vary over time? A century of evidence . Working Paper, AQR Capital Management. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3400998 . Accessed Jan 2020.

Israel, R., D. Palhares, and S. Richardson. 2018. Common factors in corporate bond returns. Journal of Investment Management 16: 17–46.

Koijen, R., T. Moskowitz, L. Pedersen, and E. Vrugt. 2018. Carry. Journal of Financial Economics 127: 197–225.

Lauterbach, B. 1989. Consumption, volatility, production volatility, spot-rate volatility, and the returns on treasury bills and bonds. Journal of Financial Economics 24: 155–179.

Ludvigson, S.C., and S. Ng. 2009. Macro factors in bond risk premia. Review of Financial Studies 22: 5027–5067.

Litterman, R., and J. Scheinkman. 1991. Common factors affecting bond returns. Journal of Fixed Income 1: 54–61.

Mazzoleni, M., and B. Kunz. 2018. When value goes global . Working Paper, Research Affiliates (March).

Moskowitz, T., Y. Ooi, and L. Pedersen. 2012. Time series momentum. Journal of Financial Eco-nomics 104: 228–250.

Siegel, L.B. 2003. Benchmarks and Investment Management . Charlottesville, VA: Research Foundation of the Institute of Chartered Financial Analysts.

Wright, J. 2011. Term premia and inflation uncertainty: Empirical evidence from an international panel dataset. American Economic Review 101: 1514–1534.

Download references

Acknowledgements

Views expressed in this paper are those of the authors and do not necessarily reflect those of Deka Investment or its employees. We acknowledge the outstanding research assistance of Gurur Akbas, and we are very grateful for the comments made by Michael Wegener.

Author information

Authors and affiliations.

International University of Monaco, Deka Investment GmbH and IQ-KAP, Mainzer Landstraße 16, 60325, Frankfurt am Main, Germany

Demir Bektić

Department of Business, Economics and Law, TH Köln University of Applied Sciences, Claudiusstrasse 1, 50678, Cologne, Germany

Britta Hachenberg

Department of Law and Economics, Technical University of Darmstadt, Hochschulstrasse 1, 64289, Darmstadt, Germany

Demir Bektić & Dirk Schiereck

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Demir Bektić .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Bektić, D., Hachenberg, B. & Schiereck, D. Factor-based investing in government bond markets: a survey of the current state of research. J Asset Manag 21 , 94–105 (2020). https://doi.org/10.1057/s41260-020-00156-3

Download citation

Published : 11 March 2020

Issue Date : March 2020

DOI : https://doi.org/10.1057/s41260-020-00156-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Government bonds
• Sovereign bonds
• Risk premia
• Style investing

JEL Classification

• Find a journal
• Publish with us
• Track your research